题目内容
已知点P为椭圆C: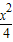 +
+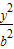 =1 (b>0)上的动点,且|OP|的最小值为1,其中O为坐标原点,则b= .
=1 (b>0)上的动点,且|OP|的最小值为1,其中O为坐标原点,则b= .
【答案】分析:根据椭圆的参数方程,设P(2cosα,bsinα),可得|OP|2= (b2+4)+(2-
(b2+4)+(2- b2)cos2α.因为|OP|的最小值为1,所以
b2)cos2α.因为|OP|的最小值为1,所以 (b2+4)-|2-
(b2+4)-|2- b2|=1,再加以讨论即可解出b的值为1.
b2|=1,再加以讨论即可解出b的值为1.
解答:解:∵点P为椭圆C: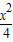 +
+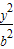 =1 (b>0)上的动点,
=1 (b>0)上的动点,
∴设P(2cosα,bsinα),可得
|OP|2=4cos2α+b2sin2α= (b2+4)+(2-
(b2+4)+(2- b2)cos2α
b2)cos2α
∵|OP|的最小值为1,得|OP|2的最小值也为1
∴ (b2+4)-|2-
(b2+4)-|2- b2|=1
b2|=1
当b2≥4时,方程化为 (b2+4)-(
(b2+4)-( b2-2)=1得4=1,无实数解;
b2-2)=1得4=1,无实数解;
当b2<4时, (b2+4)-(2-
(b2+4)-(2- b2)=1,即b2=1,解之得b=1
b2)=1,即b2=1,解之得b=1
综上所述,所求b的值为1
故答案为:1
点评:本题给出椭圆上的动点P到原点的距离最小值为1,求参数b的值.着重考查了椭圆的标准方程和简单几何性质、曲线上的点到原点最短距离求法等知识,属于中档题.
 (b2+4)+(2-
(b2+4)+(2- b2)cos2α.因为|OP|的最小值为1,所以
b2)cos2α.因为|OP|的最小值为1,所以 (b2+4)-|2-
(b2+4)-|2- b2|=1,再加以讨论即可解出b的值为1.
b2|=1,再加以讨论即可解出b的值为1.解答:解:∵点P为椭圆C:
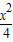 +
+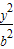 =1 (b>0)上的动点,
=1 (b>0)上的动点,∴设P(2cosα,bsinα),可得
|OP|2=4cos2α+b2sin2α=
 (b2+4)+(2-
(b2+4)+(2- b2)cos2α
b2)cos2α∵|OP|的最小值为1,得|OP|2的最小值也为1
∴
 (b2+4)-|2-
(b2+4)-|2- b2|=1
b2|=1当b2≥4时,方程化为
 (b2+4)-(
(b2+4)-( b2-2)=1得4=1,无实数解;
b2-2)=1得4=1,无实数解;当b2<4时,
 (b2+4)-(2-
(b2+4)-(2- b2)=1,即b2=1,解之得b=1
b2)=1,即b2=1,解之得b=1综上所述,所求b的值为1
故答案为:1
点评:本题给出椭圆上的动点P到原点的距离最小值为1,求参数b的值.着重考查了椭圆的标准方程和简单几何性质、曲线上的点到原点最短距离求法等知识,属于中档题.

练习册系列答案
相关题目