题目内容
一同学在电脑中打出如下若干个圈:○●○○●○○○●○○○○●○○○○○●…若将此若干个圈依此规律继续下去,得到一系列的圈,那么在前120个圈中的●的个数是 。
14;
解析试题分析:把每个实心圆和它前面的连续的空心圆看成一组,那么每组圆的总个数就等于2,3,4,…所以这就是一个等差数列.根据等差数列的求和公式可以算出第120个圆在第15组,且第120个圆不是实心圆,所以前120个圆中有14个实心圆.解:将圆分组:第一组:○●,有2个圆;第二组:○○●,有3个圆;,第三组:○○○●,有4个圆;,…,每组圆的总个数构成了一个等差数列,前n组圆的总个数为,sn=2+3+4+…+(n+1)=,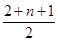 •n,令sn=120,解得n≈14.1,即包含了14整组,即有14个黑圆,故答案为14.
•n,令sn=120,解得n≈14.1,即包含了14整组,即有14个黑圆,故答案为14.
考点:等差数列
点评:解题的关键是找出图形的变化规律,构造等差数列,然后利用等差数列的求和公式计算.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
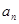 },满足
},满足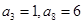 ,则此数列的前
,则此数列的前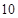 项的和
项的和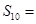 .
.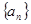 的前三项为
的前三项为 ,则此数列的通项公式为______ .
,则此数列的通项公式为______ .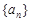 中,若
中,若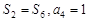 ,则
,则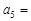 。
。 中,当
中,当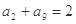 时,它的前10项和
时,它的前10项和 = .
= .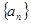 ,若
,若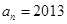 ,则
,则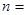 ________.
________. 的前
的前 项和为
项和为 ,若
,若 ,且
,且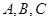 三点共线(该直线不过点
三点共线(该直线不过点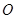 ),则
),则 _____________.
_____________.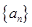 中,若
中,若 ,则该数列的前2009项的和是 .
,则该数列的前2009项的和是 .