题目内容
 祖暅原理也就是“等积原理”,它是由我国南北朝杰出的数学家、祖冲之的儿子祖暅首先提出来的.祖暅原理的内容是:夹在两个平行平面间的两个几何体,被平行于这两个平行平面的平面所截,如果截得两个截面的面积总相等,那么这两个几何体的体积相等.可以用诗句“两个胖子一般高,平行地面刀刀切,刀刀切出等面积,两人必然同样胖”形象表示其内涵.利用祖暅原理可以推导几何体的体积公式,关键是要构造一个参照体.试用祖暅原理推导球的体积公式.
祖暅原理也就是“等积原理”,它是由我国南北朝杰出的数学家、祖冲之的儿子祖暅首先提出来的.祖暅原理的内容是:夹在两个平行平面间的两个几何体,被平行于这两个平行平面的平面所截,如果截得两个截面的面积总相等,那么这两个几何体的体积相等.可以用诗句“两个胖子一般高,平行地面刀刀切,刀刀切出等面积,两人必然同样胖”形象表示其内涵.利用祖暅原理可以推导几何体的体积公式,关键是要构造一个参照体.试用祖暅原理推导球的体积公式.分析: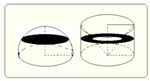 由祖暅原理的内容的提示此题可先观察V圆锥、V半球、V圆柱这三个量(等底等高)之间的不等关系,再构造一个参照体,这样的参照体我们可以用圆柱内挖去一个圆锥构造出,如图所示.接下来利用祖暅原理证明猜想.
由祖暅原理的内容的提示此题可先观察V圆锥、V半球、V圆柱这三个量(等底等高)之间的不等关系,再构造一个参照体,这样的参照体我们可以用圆柱内挖去一个圆锥构造出,如图所示.接下来利用祖暅原理证明猜想.
 由祖暅原理的内容的提示此题可先观察V圆锥、V半球、V圆柱这三个量(等底等高)之间的不等关系,再构造一个参照体,这样的参照体我们可以用圆柱内挖去一个圆锥构造出,如图所示.接下来利用祖暅原理证明猜想.
由祖暅原理的内容的提示此题可先观察V圆锥、V半球、V圆柱这三个量(等底等高)之间的不等关系,再构造一个参照体,这样的参照体我们可以用圆柱内挖去一个圆锥构造出,如图所示.接下来利用祖暅原理证明猜想.解答:解:我们先推导半球的体积.为了计算半径为R的半球的体积,我们先观察V圆锥、V半球、V圆柱这三个量(等底等高)之间的不等关系,

可以发现V圆锥<V半球<V圆柱,即
πR3<V半球<πR3,根据这一不等关系,我们可以猜测V半球=
πR3,并且由猜测可发现V半球=V圆柱-V圆锥.
下面进一步验证了猜想的可靠性.关键是要构造一个参照体,这样的参照体我们可以用圆柱内挖去一个圆锥构造出,如图所示.下面利用祖暅原理证明猜想.

证明:用平行于平面α的任意一个平面去截这两个几何体,截面分别为圆面和圆环面.
如果截平面与平面α的距离为l,那么圆面半径r=
,圆环面的大圆半径为R,小圆半径为r.
因此S圆=πr2=π(R2-l2),
S环=πR2-πl2=π(R2-l2),∴S圆=S环.
根据祖暅原理,这两个几何体的体积相等,即V半球=πR2×R-
πR2×R=
πR3,
所以V球=
πR3.

可以发现V圆锥<V半球<V圆柱,即
| 1 |
| 3 |
| 2 |
| 3 |
下面进一步验证了猜想的可靠性.关键是要构造一个参照体,这样的参照体我们可以用圆柱内挖去一个圆锥构造出,如图所示.下面利用祖暅原理证明猜想.

证明:用平行于平面α的任意一个平面去截这两个几何体,截面分别为圆面和圆环面.
如果截平面与平面α的距离为l,那么圆面半径r=
| R2-l2 |
因此S圆=πr2=π(R2-l2),
S环=πR2-πl2=π(R2-l2),∴S圆=S环.
根据祖暅原理,这两个几何体的体积相等,即V半球=πR2×R-
| 1 |
| 3 |
| 2 |
| 3 |
所以V球=
| 4 |
| 3 |
点评:本题考查祖暅原理、几何体的体积,考查转化思想,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 祖暅原理也就是“等积原理”,它是由我国南北朝杰出的数学家、祖冲之的儿子祖暅首先提出来的.祖暅原理的内容是:夹在两个平行平面间的两个几何体,被平行于这两个平行平面的平面所截,如果截得两个截面的面积总相等,那么这两个几何体的体积相等.可以用诗句“两个胖子一般高,平行地面刀刀切,刀刀切出等面积,两人必然同样胖”形象表示其内涵.利用祖暅原理可以推导几何体的体积公式,关键是要构造一个参照体.试用祖暅原理推导球的体积公式.
祖暅原理也就是“等积原理”,它是由我国南北朝杰出的数学家、祖冲之的儿子祖暅首先提出来的.祖暅原理的内容是:夹在两个平行平面间的两个几何体,被平行于这两个平行平面的平面所截,如果截得两个截面的面积总相等,那么这两个几何体的体积相等.可以用诗句“两个胖子一般高,平行地面刀刀切,刀刀切出等面积,两人必然同样胖”形象表示其内涵.利用祖暅原理可以推导几何体的体积公式,关键是要构造一个参照体.试用祖暅原理推导球的体积公式.
