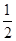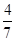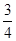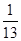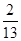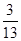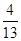题目内容
连掷两次骰子得到的点数分别为m和n,记向量a=(m , n)与向量b=(1,-1)夹角为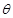 ,则
,则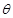
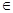 (0,
(0,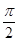 ]的概率是 ( )
]的概率是 ( )
A.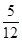 | B.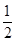 | C.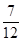 | D.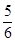 |
C
解析试题分析:由题意知本题是一个古典概型,试验发生包含的所有事件数6×6,∵m>0,n>0,
∴向量a=(m , n)与向量b=(1,-1)不可能同向.∴夹角θ≠0.∵θ∈(0,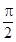 】
】
a.b≥0,∴m-n≥0,即m≥n.
当m=6时,n=6,5,4,3,2,1;
当m=5时,n=5,4,3,2,1;
当m=4时,n=4,3,2,1;
当m=3时,n=3,2,1;
当m=2时,n=2,1;
当m=1时,n=1.
∴满足条件的事件数6+5+4+3+2+1=21,故概率为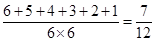 ,选C
,选C
考点:本题主要考查了向量知识,向量观点在数学.物理等学科的很多分支有着广泛的应用,而它具有代数形式和几何形式的“双重身份”能融数形于一体,能与中学数学教学内容的许多主干知识综合,形成知识交汇点.
点评:解决该试题的关键是由题意知本题是一个古典概型,根据分步计数原理可以得到试验发生包含的所有事件数,满足条件的事件数要通过列举得到,题目大部分内容考查的是向量的问题,这是一个综合题

 阅读快车系列答案
阅读快车系列答案从一批产品中取出三件产品,设A=“三件产品全不是次品”,B=“三件产品全是次品”,C=“三件产品不全是次品”,则下列结论正确的是( )
| A.A与C互斥 | B.B与C互斥 |
| C.任何两个均互斥 | D.任何两个均不互斥 |
若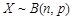 ,且
,且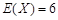 ,
,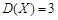 ,则
,则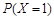 的值为( )
的值为( )
A.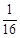 | B.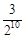 | C.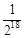 | D.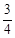 |
已知某厂的产品合格率为90%,现抽出10件产品检查,则下列说法正确的是 ( )
| A.合格产品少于9件 | B.合格产品多于9件 |
| C.合格产品正好是9件 | D.合格产品可能是9件 |
某全日制大学共有学生5600人,其中专科有1300人、本科有3000人、研究生1300人,现采用分层抽样的方法调查学生利用因特网查找学习资料的情况,抽取的样本为280人,则应在专科生、本科生与研究生这三类学生中应分别抽取( )
| A.65人,150人,65人 | B.30人,150人,100人 |
| C.93人,94人,93人 | D.80人,120人,80人 |
设随机变量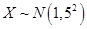 ,且
,且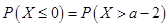 ,则实数
,则实数 的值为( )
的值为( )
| A.4 | B.6 | C.8 | D.10 |
设随机变量X ~N(2,4),则D(
~N(2,4),则D(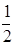 X)的值等于 ( )
X)的值等于 ( )
| A.1 | B.2 |
C.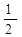 | D.4 |
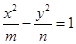 (其中
(其中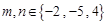 )所表示的圆锥曲线(椭圆、双曲线、抛物线)方程中任取一个,则此方程是焦点在
)所表示的圆锥曲线(椭圆、双曲线、抛物线)方程中任取一个,则此方程是焦点在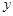 轴上的双曲线方程的概率为( )
轴上的双曲线方程的概率为( )