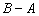题目内容
已知等比数列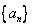 的首项为
的首项为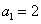 ,公比为
,公比为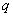 (
(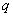 为正整数),且满足
为正整数),且满足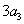 是
是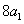 与
与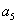 的等差中项;数列
的等差中项;数列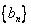 满足
满足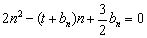 (
(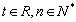 ).
).
(1)求数列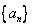 的通项公式;
的通项公式;
(2)试确定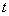 的值,使得数列
的值,使得数列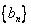 为等差数列;
为等差数列;
(3)当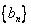 为等差数列时,对任意正整数
为等差数列时,对任意正整数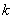 ,在
,在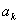 与
与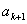 之间插入2共
之间插入2共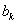 个,得到一个新数列
个,得到一个新数列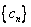 .设
.设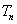 是数列
是数列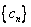 的前
的前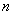 项和,试求满足
项和,试求满足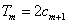 的所有正整数
的所有正整数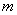 的值。
的值。
【答案】
【解析】(1)因为 ,所以
,所以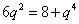 ,解得
,解得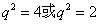 (舍),则
(舍),则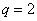 ………………3分
………………3分
又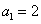 ,所以
,所以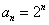 …………4分
…………4分
(2)由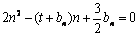 ,得
,得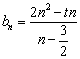 ,
,
所以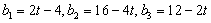 ,
,
则由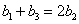 ,得
,得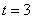
而当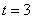 时,
时,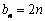 ,由
,由 (常数)知此时数列
(常数)知此时数列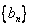 为等差数列…8分
为等差数列…8分
(3)因为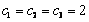 ,易知
,易知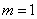 不合题意,
不合题意,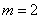 适合题意………………9分
适合题意………………9分
当 时,若后添入的数2 = cm + 1,则一定不适合题意,从而cm + 1必是数列
时,若后添入的数2 = cm + 1,则一定不适合题意,从而cm + 1必是数列 中的某一项
中的某一项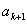 ,则
,则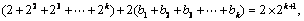
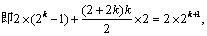 即
即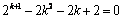 .
.
也就是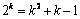 ,
,
易证k=1,2,3,4不是该方程的解,而当n≥5时,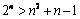 成立,证明如下:
成立,证明如下:
1°当n = 5时,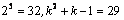 ,左边>右边成立;
,左边>右边成立;
2°假设n = k时,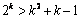 成立,
成立,
当n = k + 1时,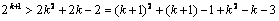
≥(k+1)2+(k+1)–1+5k–k–3=(k+1)2+(k+1)–1+k+3(k–1)
>(k+1)2+(k+1)–1
这就是说,当n=k+1时,结论成立.
由1°,2°可知,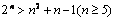 时恒成立,故
时恒成立,故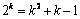 无正整数解.
无正整数解.
综上可知,满足题意的正整数仅有m=2.…………13分

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目