题目内容
已知 ,
,①若向量
 .且
.且 ∥
∥ ,求f(x)的值;
,求f(x)的值;②在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,且满足(2a-c)cosB=bcosC,求f(A)的取值范围.
【答案】分析:①利用向量共线的充要条件,可求x的值,从而可求f(x)的值;
②利用余弦定理求出B的值,确定出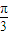 <A+
<A+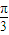 <π,然后求出函数f(A)的取值范围.
<π,然后求出函数f(A)的取值范围.
解答:解:①由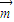 ∥
∥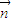 ,得
,得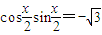
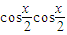 ,∴
,∴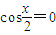 或
或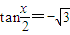 ,∴x=2kπ+π或
,∴x=2kπ+π或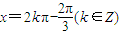 ,∴
,∴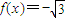
②∵(2a-c)cosB=bcosC,
由正弦定理得(2sinA-sinC)cosB=sinBcosC.∴2sinAcosB-cosBsinC=sinBcosC,
∴2sinAcosB=sin(B+C),∵A+B+C=π,∴sin(B+C)=sinA,且sinA≠0,
∴cosB= ,B=
,B=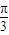 ,∴0<A<
,∴0<A<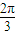 .∴
.∴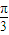 <A+
<A+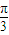 <π,0<sin(A+
<π,0<sin(A+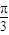 )≤1.
)≤1.
又∵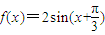 ,∴故函数f(A)的取值范围是(0,2].
,∴故函数f(A)的取值范围是(0,2].
点评:本题是中档题,考查三角函数的化简求值,考查向量共线的充要条件.
②利用余弦定理求出B的值,确定出
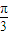 <A+
<A+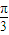 <π,然后求出函数f(A)的取值范围.
<π,然后求出函数f(A)的取值范围.解答:解:①由
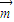 ∥
∥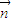 ,得
,得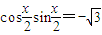
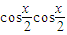 ,∴
,∴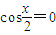 或
或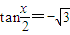 ,∴x=2kπ+π或
,∴x=2kπ+π或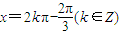 ,∴
,∴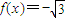
②∵(2a-c)cosB=bcosC,
由正弦定理得(2sinA-sinC)cosB=sinBcosC.∴2sinAcosB-cosBsinC=sinBcosC,
∴2sinAcosB=sin(B+C),∵A+B+C=π,∴sin(B+C)=sinA,且sinA≠0,
∴cosB=
 ,B=
,B=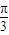 ,∴0<A<
,∴0<A<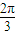 .∴
.∴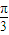 <A+
<A+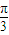 <π,0<sin(A+
<π,0<sin(A+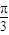 )≤1.
)≤1.又∵
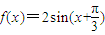 ,∴故函数f(A)的取值范围是(0,2].
,∴故函数f(A)的取值范围是(0,2].点评:本题是中档题,考查三角函数的化简求值,考查向量共线的充要条件.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
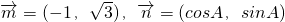 ;且
;且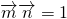 .
. ,求△ABC的面积的最大值.
,求△ABC的面积的最大值.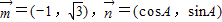 ;且
;且 .
.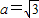 ,求△ABC的面积的最大值.
,求△ABC的面积的最大值.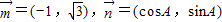 ;且
;且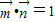 .
.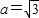 ,求△ABC的面积的最大值.
,求△ABC的面积的最大值.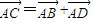 ,则ABCD为平行四边形
,则ABCD为平行四边形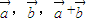 为非零向量,且a+b平分a与b的夹角,则|a|=|b|
为非零向量,且a+b平分a与b的夹角,则|a|=|b| ,
, 是非零向量,且满足
是非零向量,且满足 ,
, 。
。 ;
; ,求
,求 与
与 的夹角θ。
的夹角θ。