题目内容
将函数y=cosx的图象向左平移φ(0≤φ<2π)个单位后,得到函数y=sin 的
的
图象,则φ等于( )
A. | B. | C. | D. |
C
解析试题分析:y=cosx=sin(x+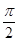 ),所以函数y=cosx的图象向左平移φ(0≤φ<2π)个单位后得y=sin(x+
),所以函数y=cosx的图象向左平移φ(0≤φ<2π)个单位后得y=sin(x+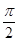 +φ),所以
+φ),所以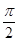 +φ=-
+φ=-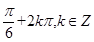 ,所以φ= -
,所以φ= -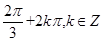 ,又因为0≤φ<2π,所以φ=
,又因为0≤φ<2π,所以φ= 。
。
考点:图像的变换;诱导公式。
点评:函数左右平移变换时,一是要注意平移方向:按“左加右减”,如由f(x)的图象变为f(x+a)(a>0)的图象,是由“x”变为“x+a”,所以是向左平移a个单位;二是要注意x前面的系数是不是1,如果不是1,左右平移时,要先提系数1,再来计算。

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
函数 导函数的图象如图所示,则下列说法正确的是( )
导函数的图象如图所示,则下列说法正确的是( )
A.函数 的递增区间为 的递增区间为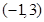 |
B.函数 的递减区间为 的递减区间为 |
C.函数 在 在 处取得极大值 处取得极大值 |
D.函数 在 在 处取得极小值 处取得极小值 |
要得到的 图象,只需将
图象,只需将 的图象 ( )
的图象 ( )
A.向左平移 个单位 个单位 | B.向右平移 个单位 个单位 |
C.向左平移 个单位 个单位 | D.向右平移 个单位 个单位 |
角 的终边经过点
的终边经过点 (
( ,
, )(
)( ),则
),则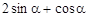 的值是( )
的值是( )
A.1或 | B. 或 或 | C.1或 | D. 或 或 |
已知函数y=cos(ωx+φ)(ω>0,|φ|<π)的部分图象如图所示,则( )
A.ω=1,φ= | B.ω=1,φ=- |
C.ω=2,φ= | D.ω=2,φ=- |
函数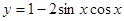 的最小正周期为( )
的最小正周期为( )
A.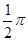 | B.π | C.2π | D.4π |
已知函数 的部分图像,则函数的解析式( )
的部分图像,则函数的解析式( )
A. | B. |
C. | D. |
已知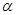 为锐角,
为锐角,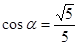 ,则
,则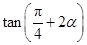 =( )
=( )
A.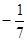 | B.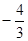 | C.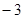 | D.-2 |
 的部分图象如右图,则
的部分图象如右图,则 ,
,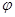 可以取的一组值是( ).
可以取的一组值是( ). 



