题目内容
函数 导函数的图象如图所示,则下列说法正确的是( )
导函数的图象如图所示,则下列说法正确的是( )
A.函数 的递增区间为 的递增区间为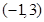 |
B.函数 的递减区间为 的递减区间为 |
C.函数 在 在 处取得极大值 处取得极大值 |
D.函数 在 在 处取得极小值 处取得极小值 |
D
解析试题分析:由于函数的图像在(1,3)为正,(3,5)为负,说明了函数递增区间为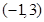 ,和
,和
递减区间为x<-1,3<x<5,因此A,B错误。
选项C中,导函数的零点为x-1,x=3,x=5,那么可知极大值是从x轴上方穿到x轴的下方的点,即为x=3,取得极大值,而在其余x=-1,x=5处取得极小值。故选D.
考点:本试题考查了导数的运用。
点评:解决该试题的关键是理解导函数的图像与函数单调性的关系,以及导数为零的点只要穿过x轴,即为极值,同时能通过导数的正负得到函数的单调增减区间,属于基础题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若 ,则tan2α等于( )
,则tan2α等于( )
A. | B. | C. | D. |
已知函数 ,点
,点 为坐标原点,点
为坐标原点,点 . 若记直线
. 若记直线 的倾斜角为
的倾斜角为 ,则
,则
A. | B. | C. | D. |
函数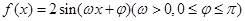 的部分图象如图所示,其 中A,B两点之间的距离为5,则f(x)的递增区间是
的部分图象如图所示,其 中A,B两点之间的距离为5,则f(x)的递增区间是
A.[6k-1,6k+2](k Z) Z) | B.[6k-4,6k-1](k Z) Z) |
C.[3k-1,4k+2](k Z) Z) | D.[3k-4,3k-1](k Z) Z) |
已知 ,则
,则 的值为( )
的值为( )
A. | B. | C. | D. |
函数 (其中
(其中 )的图象如图所示,为了得到
)的图象如图所示,为了得到 的图像,则只需将
的图像,则只需将 的图像
的图像 
A.向右平移 个长度单位 个长度单位 | B.向右平移 个长度单位 个长度单位 |
C.向左平移 个长度单位 个长度单位 | D.向左平移 个长度单位 个长度单位 |
函数 在区间
在区间 上是增函数,且
上是增函数,且 ,则
,则 ( )
( )
| A.0 | B. | C. | D.1 |
已知函数 的一部分图象如下图所示。如果
的一部分图象如下图所示。如果 ,则 ( )
,则 ( )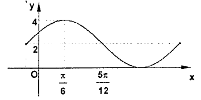
A. | B. |
C. | D. |
 的
的


