题目内容
2.点F为双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的右焦点,以F为圆心的圆过坐标原点O,且与双曲线C的两渐近线分别交于A、B两点,若四边形OAFB是菱形,则双曲线C的离心率为2.分析 由题意,△AOF是等边三角形,$\frac{b}{a}$=$\sqrt{3}$,利用双曲线C的离心率为$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$,即可得出结论.
解答 解:由题意,△AOF是等边三角形,∴$\frac{b}{a}$=$\sqrt{3}$,
∴双曲线C的离心率为$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$=$\sqrt{1+3}$=2.
故答案为:2.
点评 本题考查双曲线的方程与性质,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
13.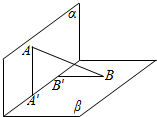 如图,平面α⊥平面β,A∈α,B∈β,AB与两平面α,β所成的角分别为$\frac{π}{4}$和$\frac{π}{6}$,线段AB在α∩β=l上的射影为 A′B′,若AB=12,则A′B′=( )
如图,平面α⊥平面β,A∈α,B∈β,AB与两平面α,β所成的角分别为$\frac{π}{4}$和$\frac{π}{6}$,线段AB在α∩β=l上的射影为 A′B′,若AB=12,则A′B′=( )
 如图,平面α⊥平面β,A∈α,B∈β,AB与两平面α,β所成的角分别为$\frac{π}{4}$和$\frac{π}{6}$,线段AB在α∩β=l上的射影为 A′B′,若AB=12,则A′B′=( )
如图,平面α⊥平面β,A∈α,B∈β,AB与两平面α,β所成的角分别为$\frac{π}{4}$和$\frac{π}{6}$,线段AB在α∩β=l上的射影为 A′B′,若AB=12,则A′B′=( )| A. | 4 | B. | 6 | C. | 8 | D. | 9 |
10.已知α∩β=l,a?α,b?β,且a,b是异面直线,那么直线l( )
| A. | 至多与a,b中的一条相交 | B. | 至少与a,b中的一条平行 | ||
| C. | 与a,b都相交 | D. | 至少与a,b中的一条相交 |
17.已知f(x)=x2-x+1,命题p:?x∈R,f(x)>0,则( )
| A. | p是真命题,¬p:?x0∈R,f(x0)<0 | B. | p是真命题,¬p:?x0∈R,f(x0)≤0 | ||
| C. | p是假命题,¬p:?x0∈R,f(x0)<0 | D. | p是假命题,¬p:?x0∈R,f(x0)≤0 |
12.关于x的方程x2+kx-k=0有两个不相等的实数根x1,x2,且满足1<x1<2<x2<3,则实数k的取值范围是( )
| A. | $({-\frac{9}{2},-4})$ | B. | $({4,\frac{9}{2}})$ | C. | (-6,-4) | D. | $({-4,\frac{4}{3}})$ |