题目内容
在△ABC中,E为AC上一点,且 ,P为BE上一点,且满足
,P为BE上一点,且满足 ,则
,则 取最小值时,向量
取最小值时,向量 的模为 .
的模为 .

解析试题分析:解: ,
,
因为 三点共线,设
三点共线,设 ,则
,则 ,其中
,其中
所以

 ,
, ,则
,则 =
= =
=
当 时,
时,
当 时,
时, ,
,  在区间
在区间 上是减函数
上是减函数
当 时,
时, ,
, 在区间
在区间 上是减函数
上是减函数
所以当 时,
时, 取得最小值,从而
取得最小值,从而 取得最小值,此时,
取得最小值,此时,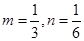
所以,
故答案应填 .
.
考点:1、向量的几何运算;2、共线向量;3、导数在研究函数性质中的应用.

练习册系列答案
相关题目
设向量 满足:
满足: .以
.以 的模为边长构成三角形,则它的边与半径为
的模为边长构成三角形,则它的边与半径为 的圆的公共点个数最多为 ( )
的圆的公共点个数最多为 ( )
A.3 | B.4 | C.5 | D.6 |
若向量a = , b =
, b = , 且a∥b ,则
, 且a∥b ,则 =
=
| A.2 | B. | C. | D. |
 中,
中, 是
是 边中点,角
边中点,角 ,
, ,
, 的对边分别是
的对边分别是 ,
, ,
, ,若
,若 ,则
,则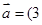 ,
, ,
, ,
, ,且
,且 ∥
∥ ,则
,则 = .
= . 上一定点,
上一定点, 是面
是面 的三个顶点,
的三个顶点, 分别是边
分别是边 对应的角.以下命题正确的序号是 .
对应的角.以下命题正确的序号是 .
 ,则
,则 ,则
,则 ,则
,则 ,则
,则 中,已知
中,已知 是
是 边上一点,
边上一点, ,则
,则 .
. +
+ =λ
=λ ,则λ= .
,则λ= . +
+ =λ
=λ ,则λ=________.
,则λ=________.