题目内容
已知A为锐角,lg(1+cosA)=m,lg
=n,则lgsinA的值为( )
| 1 |
| 1-cosA |
A、m+
| ||||
| B、m-n | ||||
C、
| ||||
D、
|
分析:把两个等式相减,根据对数函数的运算性质lga-lgb=lg
化简,因为A为锐角,根据同角三角函数间的基本关系得到lgsinA的值即可.
| a |
| b |
解答:解:两式相减得lg(l+cosA)-lg
=m-n?
lg[(1+cosA)(1-cosA)]=m-n?lgsin2A=m-n,
∵A为锐角,∴sinA>0,
∴2lgsinA=m-n,∴lgsinA=
.
故选D
| 1 |
| 1-cosA |
lg[(1+cosA)(1-cosA)]=m-n?lgsin2A=m-n,
∵A为锐角,∴sinA>0,
∴2lgsinA=m-n,∴lgsinA=
| m-n |
| 2 |
故选D
点评:此题是一道基本题,考查学生掌握对数函数的运算性质,以及利用同角三角函数间的基本关系化简求值.学生做题时应注意考虑角度的范围.

练习册系列答案
相关题目
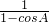 =n,则lgsinA的值为
=n,则lgsinA的值为
 (m+
(m+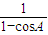 =n,则lgsinA的值为( )
=n,则lgsinA的值为( )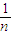
 (m+
(m+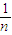 )
) (m-n)
(m-n)