题目内容
已知函数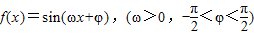 的最小正周期为π,且点
的最小正周期为π,且点 在函数的图象上.
在函数的图象上.(1)确定函数f(x)的表达式,求f(x)取得最大值时x的取值集合;
(2)求函数f(x)的单调增区间.
【答案】分析:(1)通过函数的周期求出ω,利用点在函数的图象上,ω代入函数的方程,求出φ的值,确定函数f(x)的表达式,通过正弦函数的最值求f(x)取得最大值时x的取值集合;
(2)直接利用正弦函数的单调增区间,求函数f(x)的单调增区间即可.
解答:解:(1)依题意得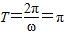 ,∴ω=2…(2分)
,∴ω=2…(2分)
将点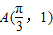 代入f(x)=sin(2x+φ)得
代入f(x)=sin(2x+φ)得 ,
,
∴ ,∴
,∴ ,
,
∵ ,∴
,∴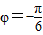 …(5分)
…(5分)
所以 ,
,
当 即
即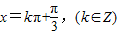 时f(x)取得最大值,
时f(x)取得最大值,
些时x的取值集合是{x|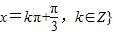 …(8分)
…(8分)
(2)由
得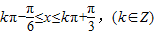 …(10分)
…(10分)
所以函数f(x)的单调增区间是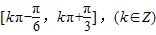 …(12分)
…(12分)
点评:本题考查函数的解析式的求法,函数的最值的应用,单调增区间的求法,考查计算能力.
(2)直接利用正弦函数的单调增区间,求函数f(x)的单调增区间即可.
解答:解:(1)依题意得
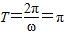 ,∴ω=2…(2分)
,∴ω=2…(2分) 将点
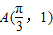 代入f(x)=sin(2x+φ)得
代入f(x)=sin(2x+φ)得 ,
,∴
 ,∴
,∴ ,
,∵
 ,∴
,∴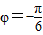 …(5分)
…(5分)所以
 ,
,当
 即
即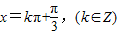 时f(x)取得最大值,
时f(x)取得最大值,些时x的取值集合是{x|
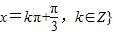 …(8分)
…(8分)(2)由

得
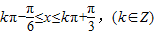 …(10分)
…(10分)所以函数f(x)的单调增区间是
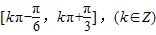 …(12分)
…(12分)点评:本题考查函数的解析式的求法,函数的最值的应用,单调增区间的求法,考查计算能力.

练习册系列答案
相关题目
 的最小正周期为
的最小正周期为 ,将其图象向左平移
,将其图象向左平移 个单位长度,所得图象关于
个单位长度,所得图象关于 轴对称,则
轴对称,则 的一个可能值是
( )
的一个可能值是
( ) B.
B. C.
C. D.
D.
 的最小正周期为2π.
的最小正周期为2π. ,求
,求 的值.
的值. 的最小正周期为π,其图象关于直线
的最小正周期为π,其图象关于直线 对称.
对称. 上的单调递增区间;
上的单调递增区间; 上只有一个实数解,求实数m的取值范围.
上只有一个实数解,求实数m的取值范围. 的最小正周期为
的最小正周期为 .
. 的值;
的值; 的最小正周期为
的最小正周期为
 的值;
的值;
 在
在
 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.