题目内容
已知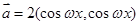 ,
, (其中
(其中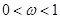 ),函数
),函数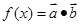 ,若直线
,若直线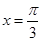 是函数
是函数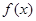 图象的一条对称轴.
图象的一条对称轴.
(Ⅰ)试求 的值;
的值;
(Ⅱ)若函数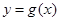 的图象是由
的图象是由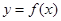 的图象的各点的横坐标伸长到原来的2倍,然后再向左平移
的图象的各点的横坐标伸长到原来的2倍,然后再向左平移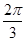 个单位长度得到,求
个单位长度得到,求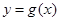 的单调递增区间.
的单调递增区间.
【答案】
(Ⅰ) 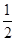 ;(Ⅱ)
;(Ⅱ) 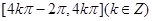 .
.
【解析】
试题分析:(Ⅰ)利用倍角公式和两角和的正弦公式化简解析式,根据函数的对称轴求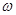 ;(Ⅱ)根据图像平移得到
;(Ⅱ)根据图像平移得到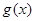 的解析式,再利用
的解析式,再利用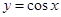 的增区间求解.
的增区间求解.
试题解析:(Ⅰ) 
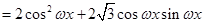
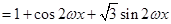
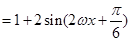 .
2分
.
2分
因为直线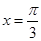 为对称轴,所以
为对称轴,所以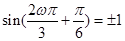 ,
,
所以
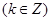 .所以
.所以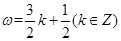 .
4分
.
4分
因为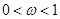 ,所以
,所以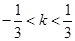 ,
,
所以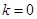 ,所以
,所以 .
6分
.
6分
(Ⅱ)由(Ⅰ)得,得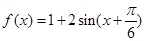 ,
,
所以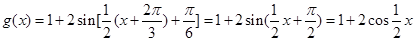 . 8分
. 8分
由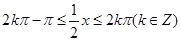 ,得
,得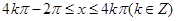 , 10分
, 10分
所以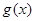 的单调递增区间为
的单调递增区间为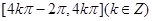 .
12分
.
12分
考点:1.倍角公式;2.正弦函数的对称轴;3.余弦函数的单调区间;4.图像平移.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 7、已知,下图是计算函数f(x)在x0处函数值的程序框图,其中a0,a1,a2,a3,a4,a5,x0是常数,且a5≠0,那么,这个函数是( )
7、已知,下图是计算函数f(x)在x0处函数值的程序框图,其中a0,a1,a2,a3,a4,a5,x0是常数,且a5≠0,那么,这个函数是( )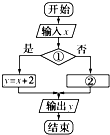 已知函数f(x)=
已知函数f(x)= ,其中
,其中 是常数,其图像是一条直线,称这个函数为线性函数,而对于非线性可导函数
是常数,其图像是一条直线,称这个函数为线性函数,而对于非线性可导函数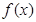 ,在已知点
,在已知点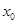 附近一点
附近一点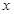 的函数值
的函数值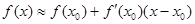 ,利用这一方法,对于实数
,利用这一方法,对于实数 ,取
,取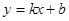 ,其中
,其中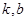 是常数,其图像是一条直线,称这个函数为线性函数,而对于非线性可导函数
是常数,其图像是一条直线,称这个函数为线性函数,而对于非线性可导函数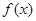 ,在已知点
,在已知点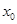 附近一点
附近一点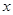 的函数值
的函数值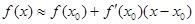 ,利用这一方法,对于实数
,利用这一方法,对于实数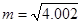 ,取
,取