题目内容
已知函数y=5cos(
πx-
)(其中k∈N),对任意实数a,在区间[a,a+3]上要使函数值
出现的次数不少于4次且不多于8次,求k值.
| 2k+1 |
| 3 |
| π |
| 6 |
| 5 |
| 4 |
分析:根据题意,可得cos(
πx-
)=
.由余弦函数的图象与性质,得当长度为3的区间大于2个周期且小于4个周期时,可使区间[a,a+3]上要使函数值
出现的次数不少于4次且不多于8次,由此建立关于k的不等式并解之,即可得到整数k的值.
| 2k+1 |
| 3 |
| π |
| 6 |
| 1 |
| 4 |
| 5 |
| 4 |
解答:解:由5cos(
πx-
)=
,得cos(
πx-
)=
.
∵函数y=cosx在每个周期内出现函数值为
的有两次,而区间[a,a+3]长度为3,
∴为了使长度为3的区间内出现函数值
不少于4次且不多于8次,
必须使3不小于2个周期长度且不大于4个周期长度.
即2×
≤3且4×
≥3,
解之得
≤k≤
.
∵k∈N,故k值为2或3.
| 2k+1 |
| 3 |
| π |
| 6 |
| 5 |
| 4 |
| 2k+1 |
| 3 |
| π |
| 6 |
| 1 |
| 4 |
∵函数y=cosx在每个周期内出现函数值为
| 1 |
| 4 |
∴为了使长度为3的区间内出现函数值
| 1 |
| 4 |
必须使3不小于2个周期长度且不大于4个周期长度.
即2×
| 2π | ||
|
| 2π | ||
|
解之得
| 3 |
| 2 |
| 7 |
| 2 |
∵k∈N,故k值为2或3.
点评:本题给出三角函数满足的条件,求参数k的取值,着重考查了三角函数的图象与性质、不等式的解法等知识,属于中档题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
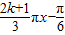 )(其中k∈N),对任意实数a,在区间[a,a+3]上要使函数值
)(其中k∈N),对任意实数a,在区间[a,a+3]上要使函数值 出现的次数不少于4次且不多于8次,求k值.
出现的次数不少于4次且不多于8次,求k值.