题目内容
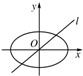 如图所示,设椭圆
如图所示,设椭圆| x2 |
| a2 |
| y2 |
| b2 |
A、 |
B、 |
C、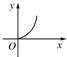 |
D、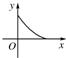 |
分析:根据椭圆的对称性,知s+t=
abπ,进而推断出s关于t的函数图象应该是斜率小于0的直线,答案可得.
| 1 |
| 2 |
解答:解:根据椭圆的对称性,知s+t=
abπ,即s=-t+
abπ,
∴关于t的函数图象应该是斜率小于0的直线
故选B
| 1 |
| 2 |
| 1 |
| 2 |
∴关于t的函数图象应该是斜率小于0的直线
故选B
点评:本题主要考查了椭圆的简单性质.考查了学生对椭圆对称的理解和掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,已知圆O:x2+y2=1,直线l:y=kx+b(b>0)是圆的一条切线,且l与椭圆
如图所示,已知圆O:x2+y2=1,直线l:y=kx+b(b>0)是圆的一条切线,且l与椭圆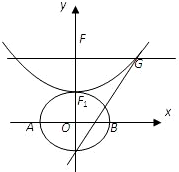 设b>0,椭圆方程为
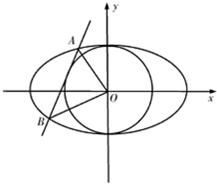
设b>0,椭圆方程为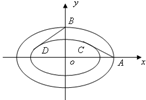 简化的北京奥运会主体育场“鸟巢”的钢结构俯视图如图所示,内外两圈的钢骨架是离心率相同的椭圆,外层椭圆顶点向内层椭圆引切线AC,BD,设内层椭圆方程为
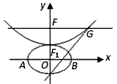
简化的北京奥运会主体育场“鸟巢”的钢结构俯视图如图所示,内外两圈的钢骨架是离心率相同的椭圆,外层椭圆顶点向内层椭圆引切线AC,BD,设内层椭圆方程为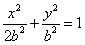 ,抛物线方程为x2=8(y-b),如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过椭圆的右焦点F1,
,抛物线方程为x2=8(y-b),如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过椭圆的右焦点F1,