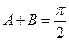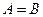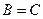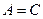题目内容
(本题满分14分) 在△ABC中, 角A, B, C所对的边分别为a, b, c, 且满足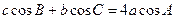 .
.
(Ⅰ) 求 的值;
的值;
(Ⅱ) 若△ABC的面积是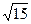 , 求
, 求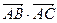 的值.
的值.
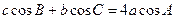 .
.(Ⅰ) 求
 的值;
的值;(Ⅱ) 若△ABC的面积是
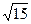 , 求
, 求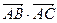 的值.
的值.(Ⅰ) 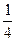 ;
;
(Ⅱ)2
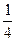 ;
;(Ⅱ)2
(Ⅰ) 利用正弦定理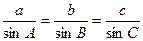 , 得
, 得
sinCcosB+sinBco sC = 4sinAcosA, sin(B+C)
sC = 4sinAcosA, sin(B+C)  = 4sinAcosA,
= 4sinAcosA,
即 sinA = 4cosAsinA, 所以cosA =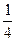 . ………………(7分)
. ………………(7分)
(Ⅱ) 由(I), 得 sinA =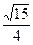 ,
,
由题意,得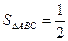 bcsinA=
bcsinA=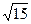 ,
,
所以bc = 8,因此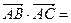 2 . ……………(14分)
2 . ……………(14分)
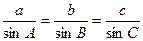 , 得
, 得sinCcosB+sinBco
 sC = 4sinAcosA, sin(B+C)
sC = 4sinAcosA, sin(B+C)  = 4sinAcosA,
= 4sinAcosA,即 sinA = 4cosAsinA, 所以cosA =
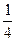 . ………………(7分)
. ………………(7分)(Ⅱ) 由(I), 得 sinA =
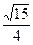 ,
,由题意,得
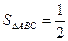 bcsinA=
bcsinA=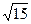 ,
,所以bc = 8,因此
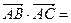 2 . ……………(14分)
2 . ……………(14分)
练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
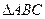 中,点M是BC的中点,
中,点M是BC的中点,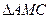 的三边长是连续三个正整数,且
的三边长是连续三个正整数,且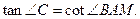
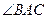 的余弦值。
的余弦值。
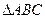 中 ,三个内角A、B、C的对边分别为a、b、c,且满足
中 ,三个内角A、B、C的对边分别为a、b、c,且满足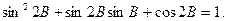
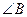 的值;
的值;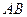 ,
,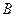 在同一水平面内的两个测点
在同一水平面内的两个测点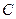 与
与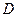 .如图所示测得
.如图所示测得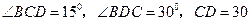 米,并在点
米,并在点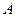 的仰角为
的仰角为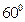 ,则塔高AB= 米。
,则塔高AB= 米。
 分别
分别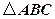 是的三个内角
是的三个内角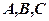 所对的边,若
所对的边,若 的( )
的( )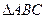 中,角A、B、C的对边分别为
中,角A、B、C的对边分别为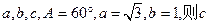 等于
等于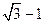 D.
D.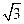
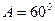 ,
,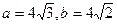 ,则B等于
,则B等于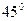 或
或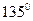 B.
B. 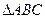 的三边长分别是
的三边长分别是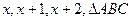 为钝角三角形,那么( )
为钝角三角形,那么( )
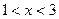
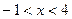
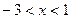
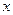 的方程
的方程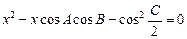 有一个根为
有一个根为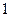 ,则△ABC中一定
,则△ABC中一定 有( )
有( )