Question

【题目】在直三棱柱ABC﹣A1B1C1中，AB=AC=1，∠BAC=90°，且异面直线A1B与B1C1所成的角等于60°，设AA1=a．

（1）求a的值；
（2）求平面A1BC1与平面B1BC1所成的锐二面角的大小．

Answer 1

【答案】
（1）∵BC∥B1C1，∴∠A1BC就是异面直线A1B与B1C1所成的角，

即∠A1BC=60°，（2分）

连接A1C，又AB=AC，则A1B=A1C∴△A1BC为等边三角形，

由AB=AC=1，∠BAC=90° ，

∴

（2）解：取A1B的中点E，连接B1E，过E作EF⊥BC1于F，

连接B1F，B1E⊥A1B，A1C1⊥B1EB1E⊥平面A1BC1B1E⊥BC1

又EF⊥BC1，所以BC1⊥平面B1EF，即B1F⊥BC1，

所以∠B1FE就是平面A1BC1与平面B1BC1所成的锐二面角的平面角．

在△B1EF中，∠B1EF=90°， ， ，∴ ∠B1FE=60°，

因此平面A1BC1与平面B1BC1所成的锐二面角的大小为60°．

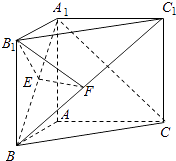
【解析】（1）将B1C1平移到BC，∠A1BC就是异面直线A1B与B1C1所成的角，在三角形A1BA内建立等式，解之即可；（2）取A1B的中点E，连接B1E，过E作EF⊥BC1于F，连接B1F，B1E⊥A1B，A1C1⊥B1E，得到∠B1FE就是平面A1BC1与平面B1BC1所成的锐二面角的平面角，在△B1EF中解出此角即可．
【考点精析】本题主要考查了平面与平面之间的位置关系的相关知识点，需要掌握两个平面平行没有交点；两个平面相交有一条公共直线才能正确解答此题．