题目内容
设x＞0，y＞0，x＋y＋xy＝2，则x＋y的最小值是（ ）
A．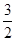
B．1 + 
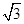C．2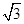－2 D．2－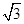
【答案】
C
【解析】
试题分析：因为x＞0，y＞0，所以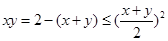
，解不等式可得x＋y的最小值是2
－2.
考点：本小题主要考查基本不等式的变形应用和二次不等式的求解.
点评：应用基本不等式及其变形公式时，要注意一正二定三相等三个条件缺一不可.
练习册系列答案
黄冈360度定制密卷系列答案
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案
相关题目