题目内容
已知动圆P过点N(2,0)并且与圆M:(x+2)2+y2=4相外切,动圆圆心P的轨迹为W,过点N的直线 与轨迹W交于A、B两点。
与轨迹W交于A、B两点。
(Ⅰ)求轨迹W的方程;
(Ⅱ)若 ,求直线
,求直线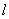 的方程;
的方程;
(Ⅲ)对于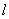 的任意一确定的位置,在直线x=
的任意一确定的位置,在直线x= 上是否存在一点Q,使得
上是否存在一点Q,使得 ,并说明理由。
,并说明理由。
 与轨迹W交于A、B两点。
与轨迹W交于A、B两点。(Ⅰ)求轨迹W的方程;
(Ⅱ)若
 ,求直线
,求直线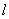 的方程;
的方程;(Ⅲ)对于
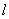 的任意一确定的位置,在直线x=
的任意一确定的位置,在直线x= 上是否存在一点Q,使得
上是否存在一点Q,使得 ,并说明理由。
,并说明理由。 解:(Ⅰ)依题意可知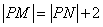 ,
,
∴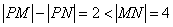 ,
,
∴点P的轨迹W是以M、N为焦点的双曲线的右支,
设其方程为 ,
,
则a=1,c=2,∴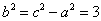 ,
,
∴轨迹W的方程为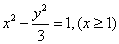 。
。
(Ⅱ)当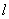 的斜率不存在时,显然不满足
的斜率不存在时,显然不满足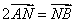 ,故
,故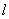 的斜率存在,
的斜率存在,
设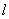 的方程为
的方程为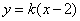 ,
,
由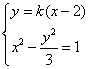 得
得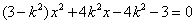 ,
,
又设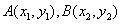 ,
,
则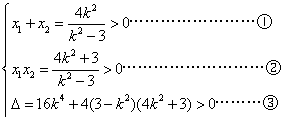 ,
,
由①②③,解得: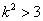 ,
,
∵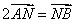 ,
,
∴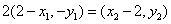 ,
,
∴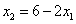 ,
,
代入①②,得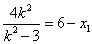 ,
,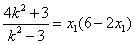 ,
,
消去x1,得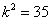 ,即
,即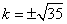 ,
,
故所求直线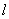 的方程为
的方程为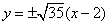 。
。
(Ⅲ)问题等价于判断以AB为直径的圆是否与直线x=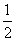 有公共点,若直线
有公共点,若直线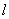 的斜率不存在,则以AB为直径的圆为
的斜率不存在,则以AB为直径的圆为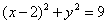 ,可知其与直线x=
,可知其与直线x=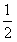 相交;
相交;
若直线 的斜率存在,则设直线
的斜率存在,则设直线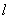 的方程为
的方程为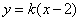 ,
,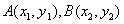 ,
,
由(Ⅱ)知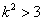 且
且 ,
,
又N(2,0)为双曲线的右焦点,双曲线的离心率e=2,
则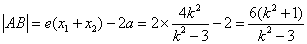 ,
,
设以AB为直径的圆的圆心为S,点S到直径x=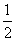 的距离为d,则
的距离为d,则
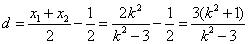 ,
,
∴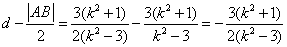 ,
,
∵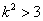 ,
,
∴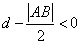 ,即
,即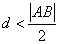 ,即直线
,即直线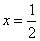 与圆S相交,
与圆S相交,
综上所述,以线段AB为直径的圆与直线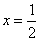 相交;
相交;
故对于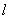 的任意一确定的位置,在直线
的任意一确定的位置,在直线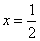 上存在一点Q(实际上存在两点)使得
上存在一点Q(实际上存在两点)使得 。
。
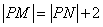 ,
,∴
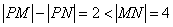 ,
,∴点P的轨迹W是以M、N为焦点的双曲线的右支,
设其方程为
 ,
,则a=1,c=2,∴
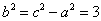 ,
,∴轨迹W的方程为
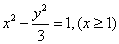 。
。 (Ⅱ)当
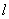 的斜率不存在时,显然不满足
的斜率不存在时,显然不满足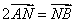 ,故
,故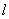 的斜率存在,
的斜率存在,设
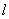 的方程为
的方程为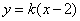 ,
,由
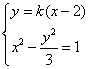 得
得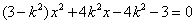 ,
,又设
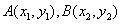 ,
,则
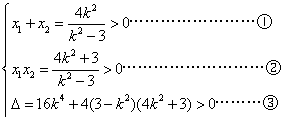 ,
,由①②③,解得:
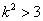 ,
,∵
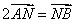 ,
,∴
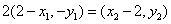 ,
,∴
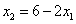 ,
,代入①②,得
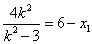 ,
,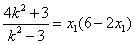 ,
,消去x1,得
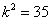 ,即
,即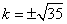 ,
,故所求直线
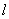 的方程为
的方程为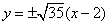 。
。(Ⅲ)问题等价于判断以AB为直径的圆是否与直线x=
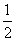 有公共点,若直线
有公共点,若直线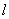 的斜率不存在,则以AB为直径的圆为
的斜率不存在,则以AB为直径的圆为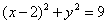 ,可知其与直线x=
,可知其与直线x=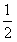 相交;
相交;若直线
 的斜率存在,则设直线
的斜率存在,则设直线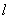 的方程为
的方程为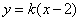 ,
,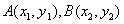 ,
,由(Ⅱ)知
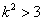 且
且 ,
,又N(2,0)为双曲线的右焦点,双曲线的离心率e=2,
则
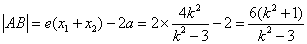 ,
,设以AB为直径的圆的圆心为S,点S到直径x=
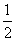 的距离为d,则
的距离为d,则 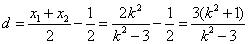 ,
,∴
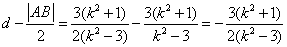 ,
,∵
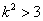 ,
,∴
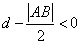 ,即
,即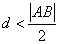 ,即直线
,即直线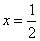 与圆S相交,
与圆S相交,综上所述,以线段AB为直径的圆与直线
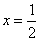 相交;
相交;故对于
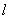 的任意一确定的位置,在直线
的任意一确定的位置,在直线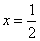 上存在一点Q(实际上存在两点)使得
上存在一点Q(实际上存在两点)使得 。
。 
练习册系列答案
相关题目
 =
=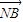 ,求直线l的方程;
,求直线l的方程; 上是否存在一点Q,使得
上是否存在一点Q,使得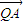 •
•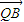 =0,并说明理由.
=0,并说明理由.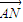 =
=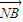 ,求直线l的方程;
,求直线l的方程; 上是否存在一点Q,使得
上是否存在一点Q,使得 •
•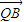 =0,并说明理由.
=0,并说明理由.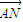 =
=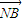 ,求直线l的方程;
,求直线l的方程; 上是否存在一点Q,使得
上是否存在一点Q,使得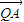 •
•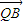 =0,并说明理由.
=0,并说明理由.