题目内容
已知动圆P过点N(2,0)并且与圆M:(x+2)2+y2=4相外切,动圆圆心P的轨迹为W,过点N的直线l与轨迹W交于A、B两点.(1)求轨迹W的方程;
(2)若2
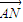 =
=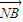 ,求直线l的方程;
,求直线l的方程;(3)对于l的任意一确定的位置,在直线x=
 上是否存在一点Q,使得
上是否存在一点Q,使得 •
•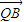 =0,并说明理由.
=0,并说明理由.
【答案】分析:(1)根据题意可推断出|PM|-|PN|=2<|MN|=4进而利用双曲线的定义可知点P的轨迹W是以M、N为焦点的双曲线的右支,设出其标准方程,依题意求得a和c,则b可求,进而求得双曲线的方程.
(2)设出l的方程与双曲线方程联立,进而利用2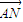 =
=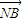 求得x2和x1的关系式,代入方程入①②求得k,则直线的方程可得.
求得x2和x1的关系式,代入方程入①②求得k,则直线的方程可得.
(3)问题可转化为判断以AB为直径的圆是否与直线x= 有公共点,先看直线l的斜率不存在,则以AB为直径的圆为(x-2)2+y2=9,可知其与直线x=
有公共点,先看直线l的斜率不存在,则以AB为直径的圆为(x-2)2+y2=9,可知其与直线x= 相交;再看斜率存在时设出直线的方程,利用焦点坐标和离心率求得|AB|的表达式,设以AB为直径的圆的圆心为S,点S到直径x=
相交;再看斜率存在时设出直线的方程,利用焦点坐标和离心率求得|AB|的表达式,设以AB为直径的圆的圆心为S,点S到直径x= 的距离为d,则d可求,d-
的距离为d,则d可求,d-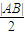 判断出结果小于0,推断出d<
判断出结果小于0,推断出d<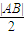 ,进而可知直线x=
,进而可知直线x= 与圆S相交,最后综合可得答案.
与圆S相交,最后综合可得答案.
解答:解:(1)依题意可知|PM|=|PN|+2∴|PM|-|PN|=2<|MN|=4,
∴点P的轨迹W是以M、N为焦点的双曲线的右支,设其方程为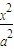 -
-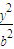 =1(a>0,b>0)则a=1,c=2,
=1(a>0,b>0)则a=1,c=2,
∴b2=c2-a2=3,∴轨迹W的方程为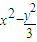 =1,(x≥1).
=1,(x≥1).
(2)当l的斜率不存在时,显然不满足2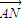 =
=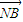 ,故l的斜率存在,设l的方程为y=k(x-2),
,故l的斜率存在,设l的方程为y=k(x-2),
由 得(3-k2)x2+4k2x-4k2-3=0,又设A(x1,y1),B(x2,y2),则
得(3-k2)x2+4k2x-4k2-3=0,又设A(x1,y1),B(x2,y2),则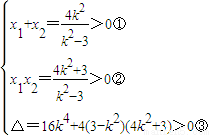
由①②③解得k2>3,∵2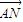 =
=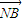 ∴2(2-x1,-y1)=(x2-2,y2)
∴2(2-x1,-y1)=(x2-2,y2)
∴x2=6-2x1代入①②得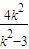 =6-x1,
=6-x1,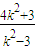 =x1(6-2x1)
=x1(6-2x1)
消去x1得k2=35,即k=±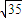 ,故所求直线l的方程为:y=±
,故所求直线l的方程为:y=±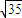 (x-2);
(x-2);
(3)问题等价于判断以AB为直径的圆是否与直线x= 有公共点
有公共点
若直线l的斜率不存在,则以AB为直径的圆为(x-2)2+y2=9,可知其与直线x= 相交;若直线l的斜率存在,则设直线l的方程为y=k(x-2),A(x1,y1),B(x2,y2)
相交;若直线l的斜率存在,则设直线l的方程为y=k(x-2),A(x1,y1),B(x2,y2)
由(2)知k2>3且x1+x2=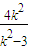 ,又N(2,0)为双曲线的右焦点,双曲线的离心率e=2,
,又N(2,0)为双曲线的右焦点,双曲线的离心率e=2,
则|AB|=e(x1+x2)-2a=2×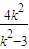 -2=
-2=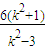
设以AB为直径的圆的圆心为S,点S到直径x= 的距离为d,则d=
的距离为d,则d=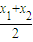 -
- =
=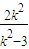 -
- =
=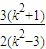
∴d-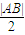 =
=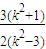 -
-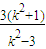 =-
=-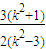
∵k2>3∴d-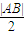 <0即d<
<0即d<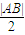 ,即直线x=
,即直线x= 与圆S相交.
与圆S相交.
综上所述,以线段AB为直径的圆与直线x= 相交;
相交;
故对于l的任意一确定的位置,与直线x= 上存在一点Q(实际上存在两点)使得
上存在一点Q(实际上存在两点)使得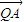 •
•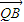 =0
=0
点评:本题主要考查了直线与圆锥曲线的综合问题.考查了学生分析问题和解决问题的能力.
(2)设出l的方程与双曲线方程联立,进而利用2
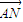 =
=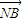 求得x2和x1的关系式,代入方程入①②求得k,则直线的方程可得.
求得x2和x1的关系式,代入方程入①②求得k,则直线的方程可得.(3)问题可转化为判断以AB为直径的圆是否与直线x=
 有公共点,先看直线l的斜率不存在,则以AB为直径的圆为(x-2)2+y2=9,可知其与直线x=
有公共点,先看直线l的斜率不存在,则以AB为直径的圆为(x-2)2+y2=9,可知其与直线x= 相交;再看斜率存在时设出直线的方程,利用焦点坐标和离心率求得|AB|的表达式,设以AB为直径的圆的圆心为S,点S到直径x=
相交;再看斜率存在时设出直线的方程,利用焦点坐标和离心率求得|AB|的表达式,设以AB为直径的圆的圆心为S,点S到直径x= 的距离为d,则d可求,d-
的距离为d,则d可求,d-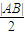 判断出结果小于0,推断出d<
判断出结果小于0,推断出d<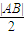 ,进而可知直线x=
,进而可知直线x= 与圆S相交,最后综合可得答案.
与圆S相交,最后综合可得答案.解答:解:(1)依题意可知|PM|=|PN|+2∴|PM|-|PN|=2<|MN|=4,
∴点P的轨迹W是以M、N为焦点的双曲线的右支,设其方程为
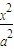 -
-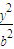 =1(a>0,b>0)则a=1,c=2,
=1(a>0,b>0)则a=1,c=2,∴b2=c2-a2=3,∴轨迹W的方程为
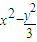 =1,(x≥1).
=1,(x≥1).(2)当l的斜率不存在时,显然不满足2
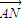 =
=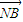 ,故l的斜率存在,设l的方程为y=k(x-2),
,故l的斜率存在,设l的方程为y=k(x-2),由
 得(3-k2)x2+4k2x-4k2-3=0,又设A(x1,y1),B(x2,y2),则
得(3-k2)x2+4k2x-4k2-3=0,又设A(x1,y1),B(x2,y2),则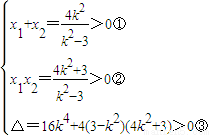
由①②③解得k2>3,∵2
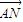 =
=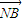 ∴2(2-x1,-y1)=(x2-2,y2)
∴2(2-x1,-y1)=(x2-2,y2)∴x2=6-2x1代入①②得
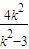 =6-x1,
=6-x1,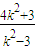 =x1(6-2x1)
=x1(6-2x1)消去x1得k2=35,即k=±
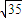 ,故所求直线l的方程为:y=±
,故所求直线l的方程为:y=±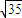 (x-2);
(x-2);(3)问题等价于判断以AB为直径的圆是否与直线x=
 有公共点
有公共点若直线l的斜率不存在,则以AB为直径的圆为(x-2)2+y2=9,可知其与直线x=
 相交;若直线l的斜率存在,则设直线l的方程为y=k(x-2),A(x1,y1),B(x2,y2)
相交;若直线l的斜率存在,则设直线l的方程为y=k(x-2),A(x1,y1),B(x2,y2)由(2)知k2>3且x1+x2=
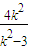 ,又N(2,0)为双曲线的右焦点,双曲线的离心率e=2,
,又N(2,0)为双曲线的右焦点,双曲线的离心率e=2,则|AB|=e(x1+x2)-2a=2×
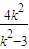 -2=
-2=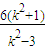
设以AB为直径的圆的圆心为S,点S到直径x=
 的距离为d,则d=
的距离为d,则d=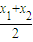 -
- =
=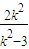 -
- =
=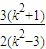
∴d-
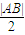 =
=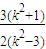 -
-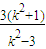 =-
=-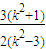
∵k2>3∴d-
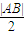 <0即d<
<0即d<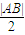 ,即直线x=
,即直线x= 与圆S相交.
与圆S相交.综上所述,以线段AB为直径的圆与直线x=
 相交;
相交;故对于l的任意一确定的位置,与直线x=
 上存在一点Q(实际上存在两点)使得
上存在一点Q(实际上存在两点)使得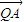 •
•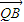 =0
=0点评:本题主要考查了直线与圆锥曲线的综合问题.考查了学生分析问题和解决问题的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 与轨迹W交于A、B两点。
与轨迹W交于A、B两点。 ,求直线
,求直线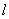 的方程;
的方程; 上是否存在一点Q,使得
上是否存在一点Q,使得 ,并说明理由。
,并说明理由。  =
=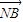 ,求直线l的方程;
,求直线l的方程; 上是否存在一点Q,使得
上是否存在一点Q,使得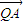 •
•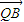 =0,并说明理由.
=0,并说明理由.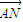 =
=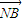 ,求直线l的方程;
,求直线l的方程; 上是否存在一点Q,使得
上是否存在一点Q,使得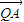 •
•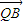 =0,并说明理由.
=0,并说明理由.