题目内容
6.已知a,b,c分别是△ABC三个内角A,B,C的所对的边,且满足(2c+b)cosA+acosB=0,若a=4则△ABC的面积的最大值是$\frac{4\sqrt{3}}{3}$.分析 已知等式利用正弦定理化简,整理后利用两角和与差的正弦函数公式及诱导公式变形,求出cosA的值,确定出sinA的值,由余弦定理列出关系式,把a,cosA的值代入并利用基本不等式求出bc的最大值,利用三角形面积公式求出三角形ABC面积的最大值即可.
解答 解:已知等式(2c+b)cosA+acosB=0,
利用正弦定理化简得:(2sinC+sinB)cosA+sinAcosB=0,
整理得:2sinCcosA+sinAcosB+cosAsinB=2sinCcosA+sin(A+B)=0,
即2sinCcosA=-sin(A+B)=-sinC,
∵sinC≠0,
∴cosA=-$\frac{1}{2}$,sinA=$\sqrt{1-co{s}^{2}A}$=$\frac{\sqrt{3}}{2}$,
由余弦定理得:a2=b2+c2-2bccosA,即16=b2+c2+bc≥2bc+bc=3bc,
∴bc≤$\frac{16}{3}$,
∴S△ABC=$\frac{1}{2}$bcsinA≤$\frac{4\sqrt{3}}{3}$,
则△ABC面积的最大值为$\frac{4\sqrt{3}}{3}$.
故答案为:$\frac{4\sqrt{3}}{3}$
点评 此题考查了正弦、余弦定理,三角形面积公式,以及基本不等式的运用,熟练掌握公式及定理是解本题的关键.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
14.一个四棱锥的三视图如图所示,那么这个四棱锥的表面积是( )
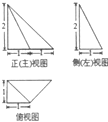

| A. | $\frac{{9+2\sqrt{3}+\sqrt{5}}}{2}$ | B. | $\frac{{9+2\sqrt{3}}}{2}$ | C. | $\frac{{9+2\sqrt{5}}}{2}$ | D. | $\frac{{11+\sqrt{5}}}{2}$ |
14.在等腰△ABC中,∠BAC=90°,AB=AC=2,$\overrightarrow{BC}=2\overrightarrow{BD}$,$\overrightarrow{AC}=3\overrightarrow{AE}$,则$\overrightarrow{AD}•\overrightarrow{BE}$的值为( )
| A. | $-\frac{4}{3}$ | B. | $-\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{4}{3}$ |
11.已知U=R,A={x|x2≤1},B={x|y=lnx},则∁U(A∪B)=( )
| A. | (-∞,0)(1,+∞) | B. | (-∞,0)(1,+∞) | C. | (-∞,-1) | D. | (-∞,-1] |
18.如图所示的程序框图的输出结果是( )


| A. | 2 | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -1 |
16.阅读如图所示的程序框图,则输出的A的值是( )


| A. | 15 | B. | 21 | C. | 28 | D. | 36 |
 已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右焦点分别为F1,F2及椭圆的短轴端点为顶点的三角形是等边三角形,椭圆的右顶点到右焦点的距离为1
已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左、右焦点分别为F1,F2及椭圆的短轴端点为顶点的三角形是等边三角形,椭圆的右顶点到右焦点的距离为1 如图,某几何体的三视图均为边长为2的正方形,则该几何体的体积是$\frac{20}{3}$.
如图,某几何体的三视图均为边长为2的正方形,则该几何体的体积是$\frac{20}{3}$.