题目内容
已知正实数x,y,z满足2x(x+
+
)=yz,则(x+
)(x+
)的最小值为
.
| 1 |
| y |
| 1 |
| z |
| 1 |
| y |
| 1 |
| z |
| 2 |
| 2 |
分析:先把已知中的式子展开,出现2x(x+
+
)=yz,代入(x+
)(x+
)的展开式中,再用基本不等式就可求出最小值.
| 1 |
| y |
| 1 |
| z |
| 1 |
| y |
| 1 |
| z |
解答:解:∵x,y,z满足2x(x+
+
)=yz,
∴2x2+
+
=yz,
又∵(x+
)(x+
)=x2+
+
+
∴(x+
)(x+
)=
+
∵x,y,z为正实数,∴
+
≥2
=
即(x+
)(x+
)≥
,当且仅当
=
时等号成立
∴(x+
)(x+
)的最小值为
.
故答案为
| 1 |
| y |
| 1 |
| z |
∴2x2+
| 2x |
| y |
| 2x |
| z |
又∵(x+
| 1 |
| y |
| 1 |
| z |
| x |
| y |
| x |
| z |
| 1 |
| yz |
∴(x+
| 1 |
| y |
| 1 |
| z |
| yz |
| 2 |
| 1 |
| yz |
∵x,y,z为正实数,∴
| yz |
| 2 |
| 1 |
| yz |
|
| 2 |
即(x+
| 1 |
| y |
| 1 |
| z |
| 2 |
| yz |
| 2 |
| 1 |
| yz |
∴(x+
| 1 |
| y |
| 1 |
| z |
| 2 |
故答案为
| 2 |
点评:本题主要考查了基本不等式的应用,做题时注意变形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
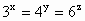 .求证:
.求证: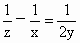 .
.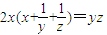 ,则
,则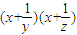 的最小值为 .
的最小值为 .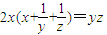 ,则
,则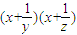 的最小值为 .
的最小值为 .