题目内容
已知正实数x,y,z满足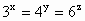 .求证:
.求证: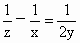 .
.
答案:略
解析:
提示:
解析:
|
由于条件中提供了相等的三个幂值,故可设其为 k,这样x、y、z都可用k表示出来,从而证出x、y、z满足的等式;另外,也可对已知等式取对数,通过变换欲证等式来证明.证法 1:设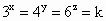 ,则 ,则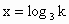 , ,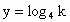 , ,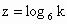 , ,
∴ 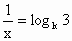 , ,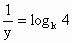 , , . .
由于 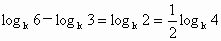 ,即 ,即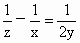 . .
证法 2:对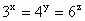 取常用对数得 取常用对数得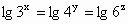 , ,
∴ x× lg3=y× lg4=z× lg6.∴ 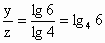 , ,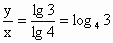 . .
于是 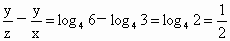 , ,
∴ 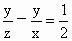 ,即 ,即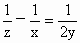 . . |
提示:
|
本题证法 1通过引入参数k,将x,y,z用同一参数k表示解题的关键;证法2通过对已知等式取对数这一等价变形形式,将等式转化为x,y,z之间的比例关系,对比结论进行变形.两种证法中,对数的运算性质与换底公式是解决本题的基础. |

练习册系列答案
相关题目
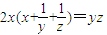 ,则
,则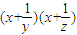 的最小值为 .
的最小值为 .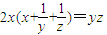 ,则
,则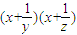 的最小值为 .
的最小值为 .