题目内容
已知等腰梯形ABCD的上底AB=3,下底CD=1,高DO=1.以高线DO为折痕,将平面ADO折起,使得平面ADO⊥平面BCDO,点H为棱AC的中点.
(1)求直线OC与直线AB所成的余弦值;
(2)求平面ADO与平面ACB所成的锐二面角的余弦值;
(3)在平面ADO内找一点G,使得GH⊥平面ACB.

(1)求直线OC与直线AB所成的余弦值;
(2)求平面ADO与平面ACB所成的锐二面角的余弦值;
(3)在平面ADO内找一点G,使得GH⊥平面ACB.

分析:(1)以O为原点,OD、OB、OA分别为x轴、y轴、z轴建立直角空间坐标系,利用
,
的夹角求解.
(2)分别求出平面ACB,平面ADO的一个法向量.利用两法向量夹角求解.
(3)要使GH⊥平面ACB,则
∥
,根据向量共线定理求出G坐标.
| OC |
| AB |
(2)分别求出平面ACB,平面ADO的一个法向量.利用两法向量夹角求解.
(3)要使GH⊥平面ACB,则
| GH |
| n |
解答:解:(1)以O为原点,OD、OB、OA分别为x轴、y轴、z轴建立直角空间坐标系.
则C(1,1,0),A(0,0,1),B(0,2,0),H(
,
,
)…(3分)∴
=(1,1,0),
=(0,2,-1)∴cos<
,
>=
…(5分)
直线OC与直线AB所成的余弦值为
;
(2)设
=(x,y,z)是平面ACB的一个法向量,又
=(1,1,-1),
=(0,2,-1)
∴
不妨取y=1,则
=(1,1,2)…(7分)
又平面ADO的一个法向量为
=(0,2,0)
∴cos<
,
>=
,即为所求 …(10分)
(3)设G(x,0,z),则
=(x-
,-
,z-
),…(12分)
要使GH⊥平面ACB,则
∥
,所以则G(0,0,-
)…(15分)
则C(1,1,0),A(0,0,1),B(0,2,0),H(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| OC |
| AB |
| OC |
| AB |
| ||
| 5 |
直线OC与直线AB所成的余弦值为
| ||
| 5 |
(2)设
| n |
| AC |
| AB |
∴
|
| n |
又平面ADO的一个法向量为
| OB |
∴cos<
| n |
| OB |
| ||
| 6 |
(3)设G(x,0,z),则
| GH |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
要使GH⊥平面ACB,则
| GH |
| n |
| 1 |
| 2 |
点评:本题考查异面直线夹角,二面角求解,直线和平面垂直关系.考查转化的思想方法(空间问题平面化)空间想象能力,计算能力.利用空间向量的知识,则使问题论证与求解演变成了代数运算,降低了思维难度,使人们解决问题更加方便.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
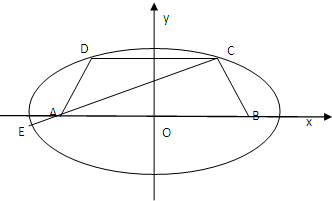 20、已知等腰梯形ABCD中,AB=2CD,
20、已知等腰梯形ABCD中,AB=2CD, ,椭圆过C、D、E三点,且以A,B为焦点.
,椭圆过C、D、E三点,且以A,B为焦点. ,求椭圆方程;
,求椭圆方程;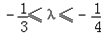 ,求椭圆离心率e的取值范围.
,求椭圆离心率e的取值范围.
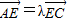 ,椭圆过C、D、E三点,且以A,B为焦点.
,椭圆过C、D、E三点,且以A,B为焦点.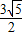 ,求椭圆方程;
,求椭圆方程;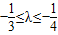 ,求椭圆离心率e的取值范围.
,求椭圆离心率e的取值范围.