题目内容
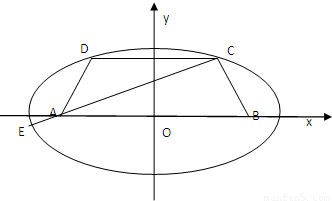
已知等腰梯形ABCD中,AB=2CD, ,椭圆过C、D、E三点,且以A,B为焦点.
,椭圆过C、D、E三点,且以A,B为焦点.
(1)若AB=4,梯形的高为 ,求椭圆方程;
,求椭圆方程;
(2)若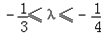 ,求椭圆离心率e的取值范围.
,求椭圆离心率e的取值范围.
 ,椭圆过C、D、E三点,且以A,B为焦点.
,椭圆过C、D、E三点,且以A,B为焦点.(1)若AB=4,梯形的高为
 ,求椭圆方程;
,求椭圆方程;(2)若
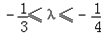 ,求椭圆离心率e的取值范围.
,求椭圆离心率e的取值范围.
解:(1)由题意,设椭圆方程为: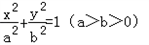 ,则c=2,
,则c=2,
把C(1,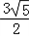 )代入椭圆方程可得:
)代入椭圆方程可得: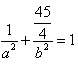 ,
,
又c2=a2-b2=4
∴a2=16,b2=12
∴椭圆方程为 ;
;
(2)设椭圆方程为: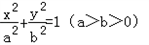 ,E(m,n),C(
,E(m,n),C( ),
),
∵A(﹣c,0),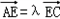 ,
,
∴E(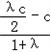 ,
,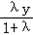 )
)
将E,C的坐标代入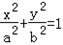 可得:
可得: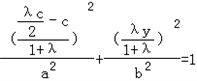 ;
;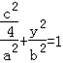
∴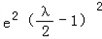 +
+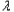 2(1﹣
2(1﹣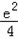 )=(1+
)=(1+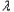 )2
)2
∴e2(1﹣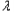 )=1+2
)=1+2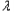
∴e2=﹣2+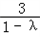
∵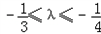
∴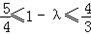
∴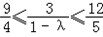
∴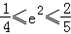
∴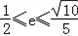
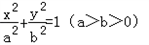 ,则c=2,
,则c=2,把C(1,
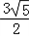 )代入椭圆方程可得:
)代入椭圆方程可得: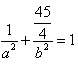 ,
,又c2=a2-b2=4
∴a2=16,b2=12
∴椭圆方程为
 ;
;(2)设椭圆方程为:
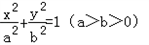 ,E(m,n),C(
,E(m,n),C( ),
),∵A(﹣c,0),
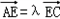 ,
,∴E(
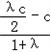 ,
,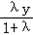 )
)将E,C的坐标代入
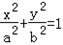 可得:
可得: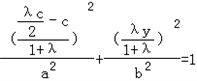 ;
;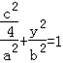
∴
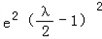 +
+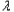 2(1﹣
2(1﹣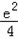 )=(1+
)=(1+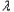 )2
)2∴e2(1﹣
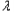 )=1+2
)=1+2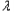
∴e2=﹣2+
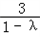
∵
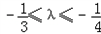
∴
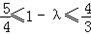
∴
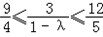
∴
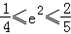
∴
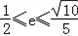

练习册系列答案
相关题目
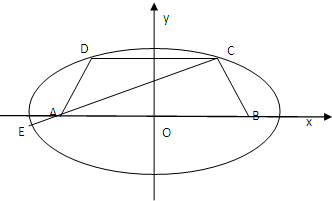 20、已知等腰梯形ABCD中,AB=2CD,
20、已知等腰梯形ABCD中,AB=2CD,
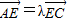 ,椭圆过C、D、E三点,且以A,B为焦点.
,椭圆过C、D、E三点,且以A,B为焦点.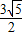 ,求椭圆方程;
,求椭圆方程;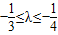 ,求椭圆离心率e的取值范围.
,求椭圆离心率e的取值范围.