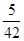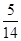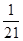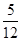Question

在1，2，3，…，9这9个自然数中，任取3个数，

(1)记Y表示“任取的3个数中偶数的个数”，求随机变量Y的分布列及其期望；

(2)记X为3个数中两数相邻的组数，例如取出的数为1，2，3，则有这两组相邻的数1，2和2，3，此时X的值为2，求随机变量X的分布列及其数学期望E(X).

 

Answer 1

【答案】

(1) 随机变量Y的分布列

Y	0	1	2	3
P

Y的期望：E（Y）=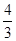

(2) X的分布列为

X	0	1	2
P

数学期望.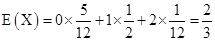

【解析】

试题分析：(1) Y服从N=9，M=4，n=3的超几何分布，∴.

Y	0	1	2	3
P

Y的期望：E（Y）=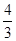

(2)X的取值为0，1，2，

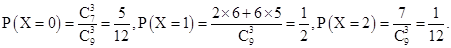
∴X的分布列为

X	0	1	2
P

数学期望.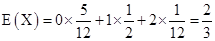

考点：超几何分布，随机变量的分布列及数学期望。

点评：中档题，统计中的抽样方法，频率直方图，概率计算及随机变量的分布列、数学期望计算问题，是高考必考内容及题型。概率的计算问题，要注意借助于排列组合知识，准确计算。