题目内容
2007年广东省实行高中等级考试,高中等级考试成绩分A,B,C,D四个等级,其中等级D为不合格,09年我校高二学生盛兴参加物理、化学、历史三科,三科合格的概率均为 ,每科得A,B,C,D 四个等级的概率分别为
,每科得A,B,C,D 四个等级的概率分别为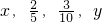 ,
,
(Ⅰ)求x,y的值;
(Ⅱ)若有一科不合格,则不能拿到高中毕业证,求学生盛兴不能拿到高中毕业证的概率;
(Ⅲ)若至少有两科得A,一科得B,就能被评为三星级学生,则学生甲被评为三星级学生的概率;
(Ⅳ)设ξ为学生盛兴考试不合格科目数,求ξ的分布列及ξ的数学期望Eξ.
解:(Ⅰ)∵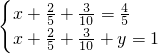 ,
,
∴ ;
;
(Ⅱ)∵三科不合格的概率均为 ,
,
∴学生盛兴不能拿到高中毕业证的概率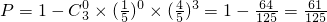 ;
;
(Ⅲ)∵每科得A,B的概率分别为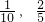 ,
,
∴学生盛兴被评为三星级学生的概率为 .
.
(Ⅳ)ξ的可能值为0,1,2,3,
∵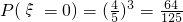 ,
,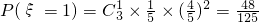 ,
,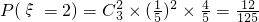 ,
, .
.
∴ξ的分布列如下表:
∴ξ的数学期望Eξ= .
.
分析:(Ⅰ)根据物理、化学、历史三科,三科合格的概率、概率的基本性质列出关于x,y的方程组,解之即得x,y的值
(Ⅱ)利用三科不合格的概率结合对立事件的概率计算公式即可求得:学生盛兴不能拿到高中毕业证的概率;
(Ⅲ)根据每科得A,B的概率结合n次独立重复试验中恰好发生k次的概率的计算公式即可求得:学生盛兴被评为三星级学生的概率;
(Ⅳ)ξ的可能值为0,1,2,3,依次求得它们的概率得出:ξ的分布列,再根据期望的计算公式即可救是ξ的数学期望.
点评:此题是个中档题.本题考查古典概型及共概率计算公式,离散型随机变量的分布列数学期望、概率的基本性质等基础知识,考查运用概率知识解决实际问题的能力.
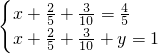 ,
,∴
 ;
;(Ⅱ)∵三科不合格的概率均为
 ,
,∴学生盛兴不能拿到高中毕业证的概率
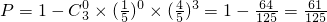 ;
;(Ⅲ)∵每科得A,B的概率分别为
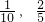 ,
,∴学生盛兴被评为三星级学生的概率为
 .
.(Ⅳ)ξ的可能值为0,1,2,3,
∵
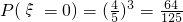 ,
,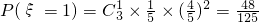 ,
,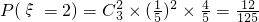 ,
, .
.∴ξ的分布列如下表:
| ξ | 0 | 1 | 2 | 3 |
| P | 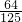 | 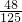 | 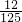 | 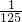 |
 .
.分析:(Ⅰ)根据物理、化学、历史三科,三科合格的概率、概率的基本性质列出关于x,y的方程组,解之即得x,y的值
(Ⅱ)利用三科不合格的概率结合对立事件的概率计算公式即可求得:学生盛兴不能拿到高中毕业证的概率;
(Ⅲ)根据每科得A,B的概率结合n次独立重复试验中恰好发生k次的概率的计算公式即可求得:学生盛兴被评为三星级学生的概率;
(Ⅳ)ξ的可能值为0,1,2,3,依次求得它们的概率得出:ξ的分布列,再根据期望的计算公式即可救是ξ的数学期望.
点评:此题是个中档题.本题考查古典概型及共概率计算公式,离散型随机变量的分布列数学期望、概率的基本性质等基础知识,考查运用概率知识解决实际问题的能力.

练习册系列答案
相关题目
 ,每科得A,B,C,D 四个等级的概率分别为
,每科得A,B,C,D 四个等级的概率分别为 ,
,