题目内容
设函数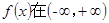 上满足以
上满足以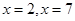 为对称轴,且在
为对称轴,且在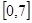 上只有
上只有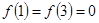 ,试求方程
,试求方程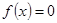 在
在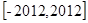 根的个数为( )
根的个数为( )
A、 803个 B、 804个 C、 805个 D、 806个
【答案】
C
【解析】本试题主要是考查了函数与方程的思想的运用,求解零点问题的综合试题。
因为函数f(x)关于x=7对称可知f(x)=f(14-x),又因为关于x=2对称,那么可知f(x)=f(4-x)故有f(4-x)=f(14-x)⇒f(x)=f(x+10),周期为10,又f(3)=f(1)=0⇒f(11)=f(13)=f(-7)=f(-9)=0,因为在闭区间[0,7]上,只有f(1)=f(3)=0,故在[4,7]上无零点,又f(7-x)=f(7+x),故在[7,10]上无零点,故在[0,10]上仅有两个解,故f(x)在[0,10]和[-10,0]上均有有两个解,从而可知函数y=f(x)在[0,2012]上有403个解,在[-2012.0]上有400个解,所以函数y=f(x)在[-2012,2012]上有805个解.故选C.
解决该试题的关键是分析在闭区间[0,7]上,只有f(1)=f(3)=0,故在[4,7]上无零点,又f(7-x)=f(7+x),故在[7,10]上无零点,故在[0,10]上仅有两个解。然后利用周期性得到结论。

练习册系列答案
相关题目
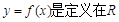 上的奇函数,且满足
上的奇函数,且满足 都成立,又
都成立,又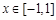 时,
时,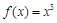 ,则下列四个命题:
,则下列四个命题: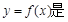 以4为周期的周期函数; ②当
以4为周期的周期函数; ②当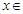 [1,3]时,
[1,3]时,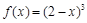 ;
;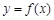 的图象关于
的图象关于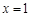 对称; ④函数
对称; ④函数