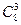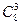题目内容
直线a、b为异面直线,直线a上有4个点,直线b上有5个点,以这些点为顶点的三角形共有________个.
70
直接法:所有三角形可以分为两类.第一类,由直线a上取2个点、直线b上取1个点所确定的三角形,共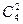 ·
·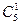 个;第二类,由直线a上取1个点、直线b上取2个点确定的三角形,共
个;第二类,由直线a上取1个点、直线b上取2个点确定的三角形,共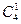 ·
·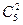 个点.所以共有三角形
个点.所以共有三角形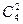 ·
·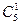 +
+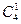 ·
·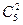 =70个.
=70个.
间接法:9个点中任取3个,共有 种取法.其中,三个点全在直线a上的有
种取法.其中,三个点全在直线a上的有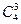 种,全在直线b上的有
种,全在直线b上的有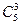 种,以它们为顶点的三角形不存在.所以,以这些点为顶点的三角形共有
种,以它们为顶点的三角形不存在.所以,以这些点为顶点的三角形共有 -
-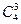 -
-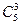 =70个.
=70个.
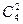 ·
·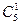 个;第二类,由直线a上取1个点、直线b上取2个点确定的三角形,共
个;第二类,由直线a上取1个点、直线b上取2个点确定的三角形,共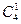 ·
·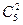 个点.所以共有三角形
个点.所以共有三角形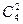 ·
·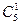 +
+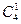 ·
·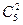 =70个.
=70个.间接法:9个点中任取3个,共有
 种取法.其中,三个点全在直线a上的有
种取法.其中,三个点全在直线a上的有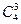 种,全在直线b上的有
种,全在直线b上的有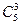 种,以它们为顶点的三角形不存在.所以,以这些点为顶点的三角形共有
种,以它们为顶点的三角形不存在.所以,以这些点为顶点的三角形共有 -
-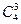 -
-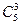 =70个.
=70个.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目