题目内容
设锐角
的三内角
、
、
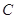所对边的边长分别为
、
、
，且 
，
,则的取值范围为（ ）
A． | B． | C． | D． |
A
解析试题分析：∵
，∴
，∴
，∴由正弦定理：
，又∵
，∴
，∵
为锐角三角形，∴
，
，
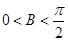，即，
，
，
∴
，∴
，∴
，∴
.
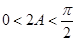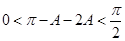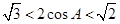考点：1.正弦定理；2.三角函数最值.
练习册系列答案
相关题目
在△ABC中，角A，B，C所对的边分别是a，b，c,若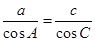
，则△ABC的形状是（ ）
| A．等腰三角形 | B．直角三角形 |
| C．等腰直角三角形 | D．等腰或直角三角形 |
中，
，则此三角形有（ ）
| A．一解 | B．两解 | C．无解 | D．不确定 |
在中，
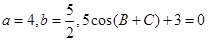，则角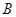
的大小为( )
A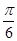． | B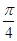． | C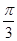． | D． |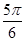
在△ABC中,若∠A=60°,∠B=45°,BC=3
,则AC等于( )
A．4 | B．2 | C． | D． |
设△ABC的内角A,B,C所对的边分别为a,b,c,若三边的长为连续的三个正整数,且A>B>C,3b=20acosA,则sinA∶sinB∶sinC为( )
| A．4∶3∶2 | B．5∶6∶7 |
| C．5∶4∶3 | D．6∶5∶4 |
如图,一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与货轮相距20海里,随后货轮按北偏西30°的方向航行,30分钟后又测得灯塔在货轮的东北方向,则货轮航行的速度为( )
A．20( + )海里/小时 | B．20(-)海里/小时 |
C．20(+ )海里/小时 | D．20(-)海里/小时 |
在△ABC中，内角A，B，C所对的边分别是a，b，c.已知8b＝5c，C＝2B，则cos C等于( )．
A． | B．－ | C．± | D． |