题目内容
定义函数![]() 其导函数记为
其导函数记为![]() .
.
(1)求证:fn(x)≥nx;
(2)设![]() ,求证:0<x0<1;
,求证:0<x0<1;
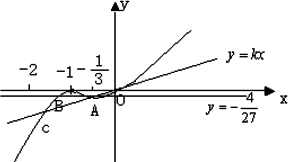
(3)是否存在区间![]() 使函数h(x)=f3(x)-f2(x)在区间[a,b]上的值域为[ka,kb]?若存在,求出最小的k值及相应的区间[a,b].
使函数h(x)=f3(x)-f2(x)在区间[a,b]上的值域为[ka,kb]?若存在,求出最小的k值及相应的区间[a,b].
答案:
解析:
解析:
|
(1)∵ 则 当 ∴ 故 ∴ (2)由 ∴ 而 由(1)知当 ∴ (3) 令 ∴当 当 当 故
下面考查直线 由图可知直线 ∵在 ∴过 |

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
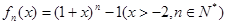 其导函数记为
其导函数记为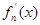 .
.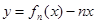 的单调递增区间;
的单调递增区间;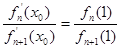 ,求证:
,求证: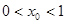 ;
;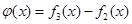 ,数列
,数列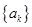 前
前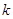 项和为
项和为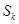 ,
, 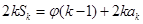 ,其中
,其中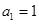 .对于给定的正整数
.对于给定的正整数 ,数列
,数列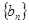 满足
满足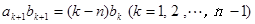 ,且
,且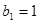 ,求
,求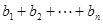 .
.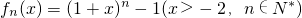 其导函数记为
其导函数记为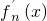 .
.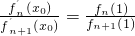 ,求证:0<x0<1;
,求证:0<x0<1;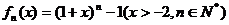 其导函数记为
其导函数记为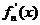 .
.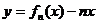 的单调递增区间;
的单调递增区间;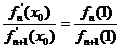 ,求证:
,求证: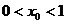 ;
;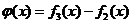 ,数列
,数列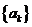 前
前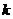 项和为
项和为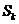 ,
,
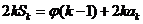 ,其中
,其中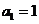 .对于给定的正整数
.对于给定的正整数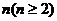 ,数列
,数列 满足
满足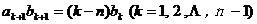 ,且
,且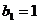 ,求
,求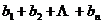 .
. 其导函数记为
其导函数记为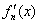 .
. ;
;
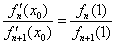 ,求证:
,求证: ;
; 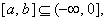 使函数
使函数 在区间
在区间 上的值域为
上的值域为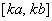 ?
若存在,求出最小的
?
若存在,求出最小的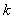 值及相应的区间
值及相应的区间