题目内容
(文)已知向量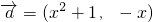 ,
,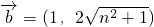 (n为正整数),函数
(n为正整数),函数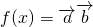 ,设f(x)在(0,+∞)上取最小值时的自变量x取值为an.
,设f(x)在(0,+∞)上取最小值时的自变量x取值为an.
(1)求数列{an}的通项公式;
(2)已知数列{bn},其中bn=an+12-an2,设Sn为数列{bn}的前n项和,求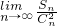 ;
;
(3)已知点列A1(1,a12)、A2(2,a22)、A3(3,a32)、…、An(n,an2)、…,设过任意两点Ai,Aj(i,j为正整数)的直线斜率为kij,当i=2008,j=2010时,求直线AiAj的斜率.
解:(1)f(x)=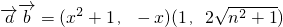 =x2-2
=x2-2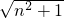 x+1(2分)
x+1(2分)
抛物线的顶点横坐标为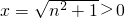 ,
,
开口向上,在(0,+∞)上当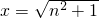 时函数取得最小值,所以
时函数取得最小值,所以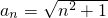 ;(4分)
;(4分)
(2)∵bn=an+12-an2=(n+1)2+1-(n2+1)=2n+1.
是首项为3,公差为2的等差数列,
所以:Sn=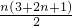 =n2+2n;
=n2+2n;
∴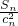 =
=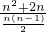 =
=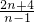 =
=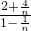 .
.
∴
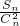 =2.
=2.
(3)∵A2008(2008,a20082),A2010(2010,2010n2),
∴k=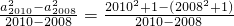 =4018.
=4018.
分析:(1)先根据向量的数量积求出f(x)的解析式,再求出f(x)在(0,+∞)上取最小值时的自变量x即可得到数列{an}的通项公式;
(2)先求出数列{bn}通项公式;进而求出前n项和Sn,代入所求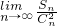 整理即可得到结论;
整理即可得到结论;
(3)先根据条件得到A2008(2008,a20082),A2010(2010,2010n2),再代入斜率的计算公式即可得到结论.
点评:本题是对数列知识与函数知识的综合考查.本题涉及到的知识比较多,有数列的极限,数列的求和,二次函数的最值等.考查计算能仪以及分析能力.
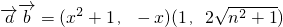 =x2-2
=x2-2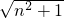 x+1(2分)
x+1(2分)抛物线的顶点横坐标为
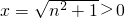 ,
,开口向上,在(0,+∞)上当
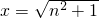 时函数取得最小值,所以
时函数取得最小值,所以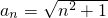 ;(4分)
;(4分)(2)∵bn=an+12-an2=(n+1)2+1-(n2+1)=2n+1.
是首项为3,公差为2的等差数列,
所以:Sn=
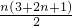 =n2+2n;
=n2+2n;∴
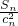 =
=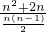 =
=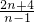 =
=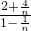 .
.∴

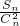 =2.
=2.(3)∵A2008(2008,a20082),A2010(2010,2010n2),
∴k=
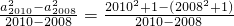 =4018.
=4018.分析:(1)先根据向量的数量积求出f(x)的解析式,再求出f(x)在(0,+∞)上取最小值时的自变量x即可得到数列{an}的通项公式;
(2)先求出数列{bn}通项公式;进而求出前n项和Sn,代入所求
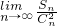 整理即可得到结论;
整理即可得到结论;(3)先根据条件得到A2008(2008,a20082),A2010(2010,2010n2),再代入斜率的计算公式即可得到结论.
点评:本题是对数列知识与函数知识的综合考查.本题涉及到的知识比较多,有数列的极限,数列的求和,二次函数的最值等.考查计算能仪以及分析能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目