题目内容
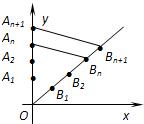 如图,在y轴的正半轴上依次有点A1,A2,…,An,…其中点A1(0,1),A2(0,10),且|An-1An|=3|AnAn+1|(n=2,3,4,…),在射线y=x(x≥0)上依次有点B1,B2,…,Bn,…点B1的坐标为(3,3),且|OBn|=|OBn-1|+2
如图,在y轴的正半轴上依次有点A1,A2,…,An,…其中点A1(0,1),A2(0,10),且|An-1An|=3|AnAn+1|(n=2,3,4,…),在射线y=x(x≥0)上依次有点B1,B2,…,Bn,…点B1的坐标为(3,3),且|OBn|=|OBn-1|+2| 2 |
(1)用含n的式子表示|AnAn+1|;
(2)用含n的式子表示An,Bn的坐标;
(3)求四边形AnAn+1Bn+1Bn面积的最大值.
分析:(1)由题意|An-1An|=3|AnAn+1|是一个等比关系,故有公式求其通项即可;
(2)由题意(1)中数列的前n项和即为An的纵坐标,由|OBn|=|OBn-1|+2
(n=2,3,4,…)知{|OBn|}是以3
为首项,2
为公差的等差数列,故可求得|OBn|的值,再由
在射线y=x(x≥0)上依次有点B1,B2,…,Bn,…即可得出Bn的坐标;
(3)根据四边形AnAn+1Bn+1Bn的几何特征,把四边形的面积分成两个三角形的面积来求,求出面积的表达式,再作差Sn+1-Sn=
<0,确定其单调性,然后求出最大值.
(2)由题意(1)中数列的前n项和即为An的纵坐标,由|OBn|=|OBn-1|+2
| 2 |
| 2 |
| 2 |
在射线y=x(x≥0)上依次有点B1,B2,…,Bn,…即可得出Bn的坐标;
(3)根据四边形AnAn+1Bn+1Bn的几何特征,把四边形的面积分成两个三角形的面积来求,求出面积的表达式,再作差Sn+1-Sn=
| 3-6n |
| 3n-1 |
解答:解:(1)∵
=
,且|A1A2|=10-1=9,∴|AnAn+1|=|A1A2|(
)n-1=9(
)n-1=(
)n-3
(2)由(1)得|A1A2|+|A2A3|+…+|An-1An|=9+3+1+…+(
)n-4=
-
(
)n-4
∴点An的坐标(0,
-
(
)n-4),∵|OBn|-|OBn-1|=2
且|OB1|=3
∵{|OBn|}是以3
为首项,2
为公差的等差数列
∴|OBn|=3
+(n-1)2
=(2n+1)
∴Bn的坐标为(2n+1,2n+1)
(3)连接AnBn+1,设四边形AnAn+1Bn+1Bn的面积为Sn,则Sn=S△AnAn+1Bn+1+S△BnBn+1An=
[(
)n-3]•(2n+3)+
•2
•[
-
(
)n-1]
=
+
,
∴Sn+1-Sn=
<0,即Sn+1<Sn,
∴{Sn}单调递减.∴Sn的最大值为S1=
+9=
.
| |AnAn+1| |
| |An-1An| |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
(2)由(1)得|A1A2|+|A2A3|+…+|An-1An|=9+3+1+…+(
| 1 |
| 3 |
| 27 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
∴点An的坐标(0,
| 29 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 2 |
∵{|OBn|}是以3
| 2 |
| 2 |
∴|OBn|=3
| 2 |
| 2 |
| 2 |
∴Bn的坐标为(2n+1,2n+1)
(3)连接AnBn+1,设四边形AnAn+1Bn+1Bn的面积为Sn,则Sn=S△AnAn+1Bn+1+S△BnBn+1An=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 29 |
| 2 |
| 27 |
| 2 |
| 1 |
| 3 |
| ||
| 2 |
| 29 |
| 2 |
| 9n |
| 3n-1 |
∴Sn+1-Sn=
| 3-6n |
| 3n-1 |
∴{Sn}单调递减.∴Sn的最大值为S1=
| 29 |
| 2 |
| 47 |
| 2 |
点评:本题是一个数列应用题,也是等差等比数列的一个综合题,本题有着一个几何背景,需要做正确的转化和归纳,才能探究出正确的解决方法.本题是个难题,比较抽象.

练习册系列答案
相关题目
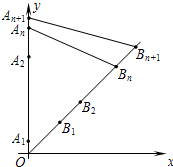 如图,在y轴的正半轴上依次有点A1、A2、…An…,其中点A1(0,1)、A2(0,10),且|An-1An|=3|AnAn+1|(n=2,3,4…),在射线y=x(x≥0)上依次有点B1、B2…、Bn…,点B1的坐标为(3,3),且|OBn|=|OBn-1|+2
如图,在y轴的正半轴上依次有点A1、A2、…An…,其中点A1(0,1)、A2(0,10),且|An-1An|=3|AnAn+1|(n=2,3,4…),在射线y=x(x≥0)上依次有点B1、B2…、Bn…,点B1的坐标为(3,3),且|OBn|=|OBn-1|+2 其中点
其中点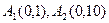 ,且
,且
 ,在射线
,在射线 上依次有
上依次有 点
点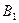 的坐
的坐 标为(3,3),且
标为(3,3),且

 的式子表示
的式子表示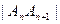 ;
;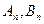 的坐标;
的坐标; 面积的最大值。
面积的最大值。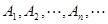 其中点
其中点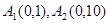 ,且
,且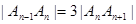
 ,在射线
,在射线 上依次有
上依次有 点
点 的坐标为(3,3),且
的坐标为(3,3),且

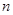 的式子表示
的式子表示 ;
;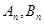 的坐标;
的坐标;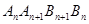 面积的最大值。
面积的最大值。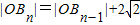 (n=2,3,4,…)
(n=2,3,4,…)