题目内容
设数列{an}是等差数列,{bn}是各项均为正数的等比数列,且a1=b1,a3+b5=21,a5+b3=13,
(1)求数列{an},{bn}的通项公式;
(2)若数列{
}的前n项和为Sn,试比较Sn与4的大小关系.
(1)求数列{an},{bn}的通项公式;
(2)若数列{
| an |
| bn |
(1)设{an}的公差为d,{bn}的公比为q,则依题意有q>0且
解得d=2,q=2.
所以an=1+(n-1)d=2n-1,bn=qn-1=2n-1.
(2)
=
.
Sn=1+
+
++
+
,①
∴2Sn=2+3+
++
+
,②
②-①得Sn=2+2+
+
++
-
=2+2×(1+
+
++
)-
=2+2×
-
=6-
.
Sn-4=2-
,
由Sn-4<0得出2n<2n+3,解得n=1,2,3,
由Sn-4>0得出2n>2n+3,解得n=4,5,6,….
所以当n≤3时Sn<4,当n≥4时Sn>4.
|
解得d=2,q=2.
所以an=1+(n-1)d=2n-1,bn=qn-1=2n-1.
(2)
| an |
| bn |
| 2n-1 |
| 2n-1 |
Sn=1+
| 3 |
| 21 |
| 5 |
| 22 |
| 2n-3 |
| 2n-2 |
| 2n-1 |
| 2n-1 |
∴2Sn=2+3+
| 5 |
| 2 |
| 2n-3 |
| 2n-3 |
| 2n-1 |
| 2n-2 |
②-①得Sn=2+2+
| 2 |
| 2 |
| 2 |
| 22 |
| 2 |
| 2n-2 |
| 2n-1 |
| 2n-1 |
=2+2×(1+
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n-2 |
| 2n-1 |
| 2n-1 |
=2+2×
1-
| ||
1-
|
| 2n-1 |
| 2n-1 |
=6-
| 2n+3 |
| 2n-1 |
Sn-4=2-
| 2n+3 |
| 2n-1 |
由Sn-4<0得出2n<2n+3,解得n=1,2,3,
由Sn-4>0得出2n>2n+3,解得n=4,5,6,….
所以当n≤3时Sn<4,当n≥4时Sn>4.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
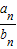 }的前n项和Sn.
}的前n项和Sn.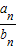 }的前n项和Sn.
}的前n项和Sn.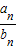 }的前n项和Sn.
}的前n项和Sn.