题目内容
 如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B在AM上,D在AN上,且对角线MN过C点,已知|AB|=3米,|AD|=2米,
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B在AM上,D在AN上,且对角线MN过C点,已知|AB|=3米,|AD|=2米,(1)设AN的长为x米,用x表示矩形AMPN的面积?
(2) 要使矩形AMPN的面积大于32平方米,则AN的长应在什么范围内?
分析:本题考查的是根据实际问题选择函数模型的问题.在解答时:
对(1)根据实际问题:由AN的长为x米,利用相似关系即可转化出边长AM,从而建立函数解析式,要注意自变量的取值范围.
对(2)利用(1)的结论由于矩形AMPN的面积大于32平方米,即可找到不等关系,变形后是解关于X在定义域内的一元二次不等式即可获得问题的解答.
对(1)根据实际问题:由AN的长为x米,利用相似关系即可转化出边长AM,从而建立函数解析式,要注意自变量的取值范围.
对(2)利用(1)的结论由于矩形AMPN的面积大于32平方米,即可找到不等关系,变形后是解关于X在定义域内的一元二次不等式即可获得问题的解答.
解答:解:(1)设AN的长为x米(x>2)
∵
=
,∴|AM|=
∴SAMPN=|AN|•|AM|=
(x>2)
(2)由SAMPN>32得
>32,
∵x>2,∴3x2-32x+64>0,即(3x-8)(x-8)>0
∴2<x<
或x>8;
AN长的取值范围是(2,
)∪(8,+∞).
∵
| |DN| |
| |AN| |
| |DC| |
| |AM| |
| 3x |
| x-2 |
∴SAMPN=|AN|•|AM|=
| 3x2 |
| x-2 |
(2)由SAMPN>32得
| 3x2 |
| x-2 |
∵x>2,∴3x2-32x+64>0,即(3x-8)(x-8)>0
∴2<x<
| 8 |
| 3 |
AN长的取值范围是(2,
| 8 |
| 3 |
点评:建立函数模型解决实际问题这类应用题的目的在于考查学生对数学语言的阅读、理解、表达与转化能力.同时也要注意实际问题中自变量的取值范围.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案
相关题目
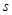 平方米,矩形一边的长为
平方米,矩形一边的长为 米(如图所示)
米(如图所示)
 平方米,矩形一边的长为
平方米,矩形一边的长为 米(如图所示)
米(如图所示)