题目内容
某人随机地将编号为1,2,3,4的四个小球放入编号为1,2,3,4的四个盒子中,每个盒子放一个小球,全部放完.(1)求编号为奇数的小球放入到编号为奇数的盒子中的概率;
(2)当一个小球放到其中一个盒子时,若球的编号与盒子的编号相同时,称该球是“放对”的,否则称该球是“放错”的,求至多有2个球“放对”的概率.
【答案】分析:(1)由排列公式,易得将4个小球放进4个盒子的情况数目,用分步计数原理可得将编号为奇数的小球放入到编号为奇数的盒子情况数目,进而由等可能事件的概率公式,计算可得答案;
(2)根据题意,分析易得至多有2个球“放对”的对立事件为4个小球全部“放对”,而4个小球全部“放对”只有1种情况,由等可能事件的概率公式可得其概率,进而由对立事件的概率的性质,可得答案.
解答:解:(1)将4个小球放进4个盒子中,有A44=24种情况,
将编号为奇数的小球放入到编号为奇数的盒子中,有A22种情况;则编号为偶数的小球必须放进编号为偶数的盒子中,也有A22种情况;则共有有A22×A22=4种情况;
故其概率P=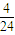 =
= ;
;
(2)至多有2个球“放对”即有2个球或1个球“放对”或没有一个球放对;进而分析可得,不会有3个小球放对的情况,则至多有2个球“放对”的对立事件为4个小球全部“放对”,
将4个小球放进4个盒子中,有A44=24种情况,4个小球全部“放对”是其中一种情况,
则4个小球全部“放对”的概率为P=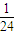 ;
;
故至多有2个球“放对”的概率为1-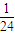 =
=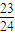 .
.
点评:本题考查等可能事件的概率,解(2)题时,需要分析事件的全部情况,进而得到至多有2个球“放对”的对立事件为4个小球全部“放对”,由对立事件的概率性质来解题.
(2)根据题意,分析易得至多有2个球“放对”的对立事件为4个小球全部“放对”,而4个小球全部“放对”只有1种情况,由等可能事件的概率公式可得其概率,进而由对立事件的概率的性质,可得答案.
解答:解:(1)将4个小球放进4个盒子中,有A44=24种情况,
将编号为奇数的小球放入到编号为奇数的盒子中,有A22种情况;则编号为偶数的小球必须放进编号为偶数的盒子中,也有A22种情况;则共有有A22×A22=4种情况;
故其概率P=
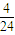 =
= ;
;(2)至多有2个球“放对”即有2个球或1个球“放对”或没有一个球放对;进而分析可得,不会有3个小球放对的情况,则至多有2个球“放对”的对立事件为4个小球全部“放对”,
将4个小球放进4个盒子中,有A44=24种情况,4个小球全部“放对”是其中一种情况,
则4个小球全部“放对”的概率为P=
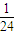 ;
;故至多有2个球“放对”的概率为1-
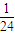 =
=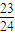 .
.点评:本题考查等可能事件的概率,解(2)题时,需要分析事件的全部情况,进而得到至多有2个球“放对”的对立事件为4个小球全部“放对”,由对立事件的概率性质来解题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 .
.