题目内容
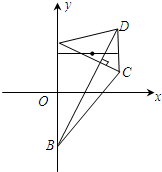
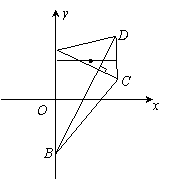
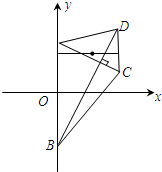 (理科)如图,梯形ABCD的底边AB在y轴上,原点O为AB的中点,|AB|=
(理科)如图,梯形ABCD的底边AB在y轴上,原点O为AB的中点,|AB|=4
| ||
| 3 |
4
| ||
| 3 |
(1)求点M的轨迹方程;
(2)过M作AB的垂线,垂足为N,若存在正常数λ0,使
| MP |
| PN |
(3)过(0,
| 1 |
| 2 |
| OP |
| OQ |
分析:(1)设点M的坐标为M(x,y)(x≠0),则 C(x,y-1+
),D(x,y+1-
),利用AC⊥BD,即
•
=0,可得轨迹方程;
(2)确定P的轨迹方程为椭圆(除去长轴的两个端点),要P到A、B的距离之和为定值,则以A、B为焦点,故1+
=
,从而可得所求P的轨迹方程;
(3)易知l的斜率存在,设方程为y=kx+
代入椭圆方程,利用
•
=0,即可求得结论.
2
| ||
| 3 |
2
| ||
| 3 |
| AC |
| BD |
(2)确定P的轨迹方程为椭圆(除去长轴的两个端点),要P到A、B的距离之和为定值,则以A、B为焦点,故1+
| 1 |
| (1+λ0)2 |
| 8 |
| 9 |
(3)易知l的斜率存在,设方程为y=kx+
| 1 |
| 2 |
| OP |
| OQ |
解答:解:(1)设点M的坐标为M(x,y)(x≠0),则 C(x,y-1+
),D(x,y+1-
)
∵A(0,
),B(0,-
),AC⊥BD
∴
•
=0,即(x,y-1)•(x,y+1)=0,
∴x2+y2=1(x≠0).
(2)设P(x,y),则M((1+λ0)x,y),代入M的轨迹方程(1+λ0)2 x2+y2=1(x≠0)
∴P的轨迹方程为椭圆(除去长轴的两个端点).
要P到A、B的距离之和为定值,则以A、B为焦点,故1+
=
,
∴λ0=2
从而所求P的轨迹方程为9x2+y2=1(x≠0).
(3)l的斜率存在,设方程为y=kx+
,代入椭圆方程可得(9+k2)x2+kx-
=0
设P(x1,y1),Q(x2,y2),则x1+x2=-
,x1x2=-
∵
•
=0,∴x1x2+y1y2=0,
整理,得
-
+
=0
∴k=±
即所求l的方程为y=±
x+
2
| ||
| 3 |
2
| ||
| 3 |
∵A(0,
2
| ||
| 3 |
2
| ||
| 3 |
∴
| AC |
| BD |
∴x2+y2=1(x≠0).
(2)设P(x,y),则M((1+λ0)x,y),代入M的轨迹方程(1+λ0)2 x2+y2=1(x≠0)
∴P的轨迹方程为椭圆(除去长轴的两个端点).
要P到A、B的距离之和为定值,则以A、B为焦点,故1+
| 1 |
| (1+λ0)2 |
| 8 |
| 9 |
∴λ0=2
从而所求P的轨迹方程为9x2+y2=1(x≠0).
(3)l的斜率存在,设方程为y=kx+
| 1 |
| 2 |
| 3 |
| 4 |
设P(x1,y1),Q(x2,y2),则x1+x2=-
| k |
| 9+k2 |
| 3 |
| 4(9+k2) |
∵
| OP |
| OQ |
整理,得
| -3(k2+1) |
| 4(9+k2) |
| k2 |
| 2(9++k2) |
| 1 |
| 4 |
∴k=±
| ||
| 2 |
即所求l的方程为y=±
| ||
| 2 |
| 1 |
| 2 |
点评:本题考查轨迹方程的求法,考查直线与椭圆的位置关系,考查向量知识的运用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 (理科)如图,梯形ABCD的底边AB在y轴上,原点O为AB的中点,|AB|=
(理科)如图,梯形ABCD的底边AB在y轴上,原点O为AB的中点,|AB|=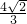 ,|CD|=2-
,|CD|=2- =λ0
=λ0 ,且P点到A、B 的距离和为定值,
,且P点到A、B 的距离和为定值, )的直线与轨迹E交于P、Q两点,且
)的直线与轨迹E交于P、Q两点,且 •
•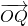 =0,求此直线方程.求点P的轨迹E的方程.
=0,求此直线方程.求点P的轨迹E的方程.