题目内容
(14分) (理科)如图,梯形ABCD的底边AB在y轴上,原点O为AB的中点,
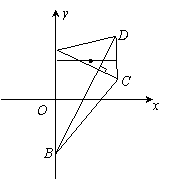
![]() M为CD的中点.
M为CD的中点.
(1)求点M的轨迹方程;
(2)过M作AB的垂线,垂足为N,若存在正常数![]() ,
,
使![]() ,且P点到A、B 的距离和为定值,
,且P点到A、B 的距离和为定值,
求点P的轨迹E的方程;
(3)过![]() 的直线与轨迹E交于P、Q两点,且
的直线与轨迹E交于P、Q两点,且![]() ,求此直线方程.
,求此直线方程.
(14分) (理科)解:(1)设点M的坐标为M(x, y)(x≠0),则![]()
又![]() 由AC⊥BD有
由AC⊥BD有![]() ,
,
即![]() ,∴x2+y2=1(x≠0). ……………………… 4分
,∴x2+y2=1(x≠0). ……………………… 4分
(2)设P(x, y),则![]() ,代入M的轨迹方程有
,代入M的轨迹方程有![]()
即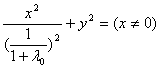 ,∴P的轨迹方程为椭圆(除去长轴的两个端点).
,∴P的轨迹方程为椭圆(除去长轴的两个端点).
要P到A、B的距离之和为定值,则以A、B为焦点,故![]()
∴![]() 从而所求P的轨迹方程为9x2+y2=1(x≠0). ………………… 8分
从而所求P的轨迹方程为9x2+y2=1(x≠0). ………………… 8分
(3)易知l的斜率存在,设方程为![]()
联立9x2+y2=1,有![]()
设P(x1, y1), Q(x2, y2),则![]() .
.
∵![]() ,而
,而![]()
∴![]() . 整理,得
. 整理,得![]()
∴![]() 即所求l的方程为
即所求l的方程为![]() ……………………… 14分
……………………… 14分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
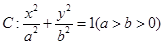 ,过焦点且垂直于长轴的弦长为1,且焦点与短轴两端点构成等边三角形.
,过焦点且垂直于长轴的弦长为1,且焦点与短轴两端点构成等边三角形.
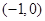 的直线
的直线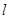 交椭圆于
交椭圆于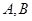 两点,交直线
两点,交直线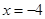 于点
于点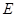 ,且
,且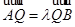 ,
,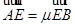 ,
,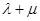 为定值,并计算出该定值.
为定值,并计算出该定值. 的底面
的底面 是直角梯形,
是直角梯形,  ,
, ,
, 为正三角形,
为正三角形, ,
, .如图4所示.
.如图4所示.
 平面
平面 .
.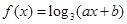 的图象经过点
的图象经过点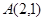 和
和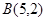 ,记
,记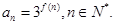
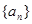 的通项公式;
的通项公式;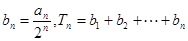 ,若
,若 ,求
,求 的最小值;
的最小值;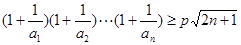 对一切
对一切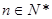 均成立的最大实数
均成立的最大实数 .
. .
. 
 ,AA1 =
,AA1 = ,M为侧棱CC1上一点,AM⊥BA1.
,M为侧棱CC1上一点,AM⊥BA1.