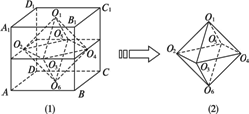
题目内容
(1)连结正方体的相邻各面的中心(所谓中心是指各面所在正方形的两条对角线的交点),所得的一个几何体是几面体?画图表示该几何体;
(2)连结上述所得的几何体的相邻各面的中心,试问所得的几何体又是几面体?
答案:
解析:
提示:
解析:
|
答案:(1)先画出正方体,然后取各个面的中心,并依次连成线,然后观察即可. 如图(1),正方体ABCD-A1B1C1D1中,O1、O2、O3、O4、O5、O6分别是各表面的中心.由点O1、O2、O3、O4、O5、O6组成了一个八面体,而且该八面体共有6个顶点,12条棱. 该多面体的图形如图(2)所示.
思路解析:连结相应点后,可以看到,由正方体的部分顶点可构成多种形状的简单几何体.如多面体ACB1D1便为四面体,即三棱锥,它是面数最少的空间几何体,而且该四面体也是正四面体;又如多面体A1ABD也是四面体,它是一个直角四面体,它也可看作是由正方体截下一个角所得的几何体,且截面是一个等边三角形. |
提示:
|
(1)在画图时要分清“虚实”,否则会使图直观性不强,导致解题错误.“后面的”被前面平面所遮住的线,如图中的O1O5、O6O5、O5O2、O5O4应画成虚线. (2)为了增强立体效果,正方体需画得“正”些,而八面体的放置应稍微“倾斜”些,这样,立体效果会更强. (3)单独画一个正八面体,应注意到,八面体可看成是由两个全等的四棱锥经重合底面后得到的,而且中间一个四边形O2O3O4O5还是正方形,当然其他的如O1O2O6O4等也是正方形. |

练习册系列答案
相关题目