题目内容
已知椭圆的两焦点为F1(-1,0)、F2(1,0),P为椭圆上一点,且2|F1F2|=|PF1|+|PF2|.
(1)求此椭圆的方程;
(2)若点P在第二象限,∠F2F1P=120°,求△PF1F2的面积.
(1)求此椭圆的方程;
(2)若点P在第二象限,∠F2F1P=120°,求△PF1F2的面积.
分析:(1)根据2|F1F2|=|PF1|+|PF2|,求出a,结合焦点坐标求出c,从而可求b,即可得出椭圆方程;
(2)求出直线方程与椭圆方程联立,可得P的坐标,利用三角形的面积公式,可求△PF1F2的面积.
(2)求出直线方程与椭圆方程联立,可得P的坐标,利用三角形的面积公式,可求△PF1F2的面积.
解答:解:(1)依题意得|F1F2|=2,
又2|F1F2|=|PF1|+|PF2|,
∴|PF1|+|PF2|=4=2a,
∴a=2,
∵c=1,
∴b2=3.
∴所求椭圆的方程为
+
=1.----------(3分)
(2)设P点坐标为(x,y),
∵∠F2F1P=120°,
∴PF1所在直线的方程为y=(x+1)•tan 120°,
即y=-
(x+1).----------(4分)
解方程组
并注意到x<0,y>0,可得
---------(6分)
∴S△PF1F2=
|F1F2|•
=
.----------(8分)
又2|F1F2|=|PF1|+|PF2|,
∴|PF1|+|PF2|=4=2a,
∴a=2,
∵c=1,
∴b2=3.
∴所求椭圆的方程为
| x 2 |
| 4 |
| y 2 |
| 3 |
(2)设P点坐标为(x,y),
∵∠F2F1P=120°,
∴PF1所在直线的方程为y=(x+1)•tan 120°,
即y=-
| 3 |
解方程组
|
并注意到x<0,y>0,可得
|
∴S△PF1F2=
| 1 |
| 2 |
3
| ||
| 5 |
3
| ||
| 5 |
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查学生的计算能力,确定P的坐标是关键.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 的左焦点为F,A(-a,0),B(0,b)为椭圆的两个顶点,若F到AB的距离等于
的左焦点为F,A(-a,0),B(0,b)为椭圆的两个顶点,若F到AB的距离等于 ,则椭圆的离心率为( )
,则椭圆的离心率为( )
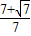


 的右焦点为F(2,0),M为椭圆的上顶点,O为坐标原点,且△MOF是等腰直角三角形.
的右焦点为F(2,0),M为椭圆的上顶点,O为坐标原点,且△MOF是等腰直角三角形. ).
). 的左焦点为F,A(-a,0),B(0,b)为椭圆的两个顶点,若F到AB的距离等于
的左焦点为F,A(-a,0),B(0,b)为椭圆的两个顶点,若F到AB的距离等于 ,则椭圆的离心率为( )
,则椭圆的离心率为( )



 的右焦点为F(2,0),M为椭圆的上顶点,O为坐标原点,且△MOF是等腰直角三角形.
的右焦点为F(2,0),M为椭圆的上顶点,O为坐标原点,且△MOF是等腰直角三角形. ).
). 的左焦点为F,A(-a,0),B(0,b)为椭圆的两个顶点,若F到AB的距离等于
的左焦点为F,A(-a,0),B(0,b)为椭圆的两个顶点,若F到AB的距离等于 ,则椭圆的离心率为( )
,则椭圆的离心率为( )


