题目内容
某电影院第一排共有 个座位,现有
个座位,现有 名观众就座,若他们每两人都不能相邻且要求每人左右至多只有两个空位,那么不同的坐法种数共有 ( )
名观众就座,若他们每两人都不能相邻且要求每人左右至多只有两个空位,那么不同的坐法种数共有 ( )
A. | B. | C. | D. |
C
解析试题分析:根据题意,由于电影院第一排共有 个座位,现有
个座位,现有 名观众就座,若他们每两人都不能相邻且要求每人左右至多只有两个空位,先排列3个人有
名观众就座,若他们每两人都不能相邻且要求每人左右至多只有两个空位,先排列3个人有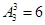 ,然后对于空位分情况可知有4种那么利用分步计数园里得到共有24种,故答案为C.
,然后对于空位分情况可知有4种那么利用分步计数园里得到共有24种,故答案为C.
考点:排列组合
点评:主要是考查了排列组合的运用,属于基础题。

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
(1-x)3(1- )3展开式中常数项是( )
)3展开式中常数项是( )
| A.-20 | B.18 | C.20 | D.0 |
用1,2,3三个数字组成一个四位数字,规定这三个数必须同时使用,且同一数字不能相邻出现,这样的四位数共有
| A.18个 | B.9个 | C.12个 | D.24个 |
某餐厅有 四个桌子,每个桌子最多坐8人,现有11人进入餐厅,随意的坐下吃饭,已知
四个桌子,每个桌子最多坐8人,现有11人进入餐厅,随意的坐下吃饭,已知 桌一定有人坐,其他桌子可能有人坐,也可能没人坐,则四个桌子坐的人数的不同的情况有多少种( )
桌一定有人坐,其他桌子可能有人坐,也可能没人坐,则四个桌子坐的人数的不同的情况有多少种( )
| A.286 | B.276 | C.264 | D.246 |
把一同排6张座位编号为1,2,3,4,5,6的电影票全部分给4个人,每人至少分1张,至多分2张,且这两张票具有连续的编号,那么不同的分法种数是
| A.168 | B.96 | C.72 | D.144 |
(1+2x) 6的展开式中,x的系数等于 ,则函数
,则函数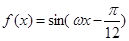 的最小正周期是
的最小正周期是
A. | B. | C. | D. |
由数字1、2、3、4、5组成没有重复数字,且3与4相邻,1与2不相邻的五位数的个数为( )
| A.1120 | B.48 | C.24 | D.12 |
 的值由右上面程序框图算出,则二项式
的值由右上面程序框图算出,则二项式 展开式的常数项为 ( )
展开式的常数项为 ( )



