题目内容
一圆形餐桌依次有A、B、C、D、E、F共有6个座位.现让3个大人和3 个小孩入座进餐,要求任何两个小孩都不能坐在一起,则不同的入座方法总 数为( )
(A)6 (B)12 (C)72 (D)144
C
解析试题分析:第一步:先从6个座位中选择3个不相邻的排列大人,有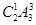 种方法,第二步:安排3个小孩有
种方法,第二步:安排3个小孩有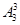 种方法,因此排列6人有
种方法,因此排列6人有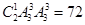 种方法
种方法
考点:排列组合
点评:不相邻问题一般采用插空法,排列完其余元素后将不相邻元素插空

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
从6名学生中选3名分别担任数学、物理、化学科代表,若甲、乙2人至少有一人入选,则不同的方法有( )
| A.40种 | B.60种 | C.96种 | D.120种 |
若 ,则
,则 的值为
的值为
A. | B.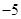 | C. | D. |
如果 的展开式中各项系数之和为128,则展开式中
的展开式中各项系数之和为128,则展开式中 的系数是 ( )
的系数是 ( )
| A.-2835 | B.2835 | C.21 | D.-21 |
有甲、乙、丙三项任务,甲需2人承担,乙、丙各需1人承担,从10人中选派4人承担这三项任务的不同选法有 ( )
| A.1260种 | B.2025种 | C.2520种 | D.5040种 |
二项式 的展开式中含
的展开式中含 项的系数为( )
项的系数为( )
A.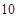 | B. | C. | D. |
已知(1+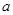 x)(1+x)5的展开式中x2的系数为5,则
x)(1+x)5的展开式中x2的系数为5,则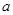 =
=
| A.-4 | B.-3 | C.-2 | D.-1 |
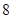 个座位,现有
个座位,现有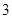 名观众就座,若他们每两人都不能相邻且要求每人左右至多只有两个空位,那么不同的坐法种数共有 ( )
名观众就座,若他们每两人都不能相邻且要求每人左右至多只有两个空位,那么不同的坐法种数共有 ( ) 






