题目内容

已知函数y=xn2-2n-3（n∈Z）的图象与两坐标轴都无公共点，且其图象关于y轴对称，求n的值，并画出函数图象．
分析：由题意可得，可得幂指数n2-2n-3为负数，且为偶数．由于当n=1时，幂指数n2-2n-3=-4，满足条件，可得函数的解析式，从而得到函数的图象．
解答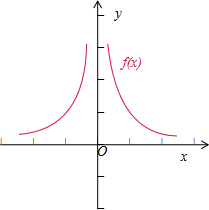：精英家教网解：已知函数y=xn2-2n-3（n∈Z）的图象与两坐标轴都无公共点，且其图象关于y轴对称，
可得幂指数n2-2n-3为负数，且为偶数．
由于当n=1时，幂指数n2-2n-3=-4，满足条件，故函数为y=x-4，
它的图象如图所示：
点评：本题主要考查幂函数的图象和性质，属于基础题．
练习册系列答案
相关题目
已知函数f（x） 定义在（-1，1）上，f（
1
2
）=1，满足f（x）-f（y）=f（
x-y
1-xy
），且数列x1=
1
2
，xn+1=
2xn
1+xn2
．
（Ⅰ）证明：f（x）在（-1，1）上为奇函数；
（Ⅱ）求f（xn）的表达式；
（Ⅲ）若a1=1，an+1=
12n
2n
f（xn）-an，（n∈N+）．试求an．
已知函数f（x）=x2-4，设曲线y=f（x）在点（xn，f（xn））处的切线与x轴的交点为（xn+1，0）（n∈N*），其中x1＞0，则xn+1与xn的关系正确的是（　　）
已知函数f（x） 定义在（-1，1）上，f（
1
2
）=1，满足f（x）-f（y）=f（
x-y
1-xy
），且数列x1=
1
2
，xn+1=
2xn
1+xn2
．
（Ⅰ）证明：f（x）在（-1，1）上为奇函数；
（Ⅱ）求f（xn）的表达式；
（Ⅲ）若a1=1，an+1=
12n
2n
f（xn）-an，（n∈N+）．试求an．

已知函数y＝xn2－2n－3(n∈Z)的图象与两坐标轴都无公共点，且其图象关于y轴对称，求n的值，并画出函数的图象．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网