题目内容
设p:f(x)=ex+lnx+2x2+mx+1在(0,+∞)内单调递增,q:m≥-5,则p是q的( )A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
【答案】分析:首先求出函数的导数,然后根据导数与函数单调性的关系求出m的范围.
解答:解:由题意得f′(x)=ex+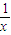 +4x+m,
+4x+m,
∵f(x)=ex+lnx+2x2+mx+1在(0,+∞)内单调递增,
∴f′(x)≥0,即ex+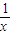 +4x+m≥0在定义域内恒成立,
+4x+m≥0在定义域内恒成立,
由于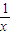 +4x≥4,当且仅当
+4x≥4,当且仅当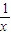 =4x,即x=
=4x,即x= 时等号成立,故对任意的x∈(0,+∞),必有ex+
时等号成立,故对任意的x∈(0,+∞),必有ex+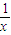 +4x>5
+4x>5
∴m≥-ex- -4x不能得出m≥-5
-4x不能得出m≥-5
但当m≥-5时,必有ex+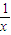 +4x+m≥0成立,即f′(x)≥0在x∈(0,+∞)上成立
+4x+m≥0成立,即f′(x)≥0在x∈(0,+∞)上成立
∴p不是q的充分条件,p是q的必要条件,即p是q的必要不充分条件
故选B.
点评:本题考查函数导数与单调性的关系.属于函数恒成立问题,难度较大,综合性强,尤其是充分条件的证明是本题的难点,本题易因为判断不出最值而导致无法下手,本解答通过给出ex+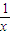 +4x>5这一条件避免了利用导数求最值,从而达到判断两个命题之间关系的目的.做题时要注意掌握此类变通的技巧.
+4x>5这一条件避免了利用导数求最值,从而达到判断两个命题之间关系的目的.做题时要注意掌握此类变通的技巧.
解答:解:由题意得f′(x)=ex+
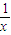 +4x+m,
+4x+m,∵f(x)=ex+lnx+2x2+mx+1在(0,+∞)内单调递增,
∴f′(x)≥0,即ex+
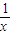 +4x+m≥0在定义域内恒成立,
+4x+m≥0在定义域内恒成立,由于
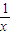 +4x≥4,当且仅当
+4x≥4,当且仅当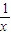 =4x,即x=
=4x,即x= 时等号成立,故对任意的x∈(0,+∞),必有ex+
时等号成立,故对任意的x∈(0,+∞),必有ex+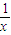 +4x>5
+4x>5∴m≥-ex-
 -4x不能得出m≥-5
-4x不能得出m≥-5但当m≥-5时,必有ex+
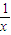 +4x+m≥0成立,即f′(x)≥0在x∈(0,+∞)上成立
+4x+m≥0成立,即f′(x)≥0在x∈(0,+∞)上成立∴p不是q的充分条件,p是q的必要条件,即p是q的必要不充分条件
故选B.
点评:本题考查函数导数与单调性的关系.属于函数恒成立问题,难度较大,综合性强,尤其是充分条件的证明是本题的难点,本题易因为判断不出最值而导致无法下手,本解答通过给出ex+
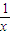 +4x>5这一条件避免了利用导数求最值,从而达到判断两个命题之间关系的目的.做题时要注意掌握此类变通的技巧.
+4x>5这一条件避免了利用导数求最值,从而达到判断两个命题之间关系的目的.做题时要注意掌握此类变通的技巧. 
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设p:f(x)=ex+lnx+2x2+mx+1在(0,+∞)内单调递增,q:m≥-5,则p是q的( )
| A、充分不必要条件 | B、必要不充分条件 | C、充分必要条件 | D、既不充分也不必要条件 |