题目内容
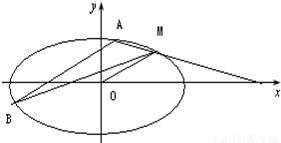
如图,已知椭圆C的中心在原点,其一个焦点与抛物线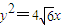 的焦点相同,又椭圆C上有一点M(2,1),直线l平行于OM且与椭圆C交于A、B两点,连MA、MB.
的焦点相同,又椭圆C上有一点M(2,1),直线l平行于OM且与椭圆C交于A、B两点,连MA、MB.(1)求椭圆C的方程.
(2)当MA、MB与x轴所构成的三角形是以x轴上所在线段为底边的等腰三角形时,求直线l在y轴上截距的取值范围.
【答案】分析:(1)抛物线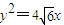 的焦点
的焦点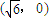 ,又椭圆C上有一点M(2,1),由此可求出椭圆方程.
,又椭圆C上有一点M(2,1),由此可求出椭圆方程.
(2)设直线在y轴上的截距为m,则直线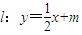 ,由直线l与椭圆C交于A、B两点,可导出m的取值范围是{m|-2<m<2且m≠0},设MA、MB的斜率分别为K1,K2,K1+K2=0,然后结合题设条件和根与系数的关系知MA,MB与x轴始终围成等腰三角形,从而得到m的取值范围.
,由直线l与椭圆C交于A、B两点,可导出m的取值范围是{m|-2<m<2且m≠0},设MA、MB的斜率分别为K1,K2,K1+K2=0,然后结合题设条件和根与系数的关系知MA,MB与x轴始终围成等腰三角形,从而得到m的取值范围.
解答:解:(1)抛物线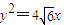 的焦点
的焦点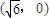 ,又椭圆C上有一点M(2,1)∴椭圆方程为,
,又椭圆C上有一点M(2,1)∴椭圆方程为,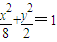
(2)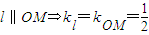 ,设直线在y轴上的截距为m,则直线
,设直线在y轴上的截距为m,则直线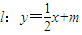
直线l与椭圆C交于A、B两点,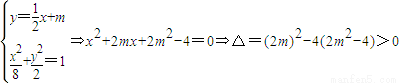
∴m的取值范围是{m|-2<m<2且m≠0},设MA、MB的斜率分别为K1,K2,∴K1+K2=0,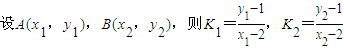 ∵
∵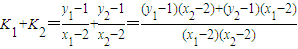
=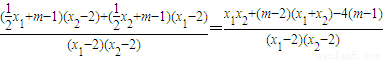
=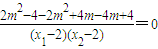
故MA,MB与x轴始终围成等腰三角形.∴m的取值范围是{m|-2<m<2且m≠0}
点评:本题考查直线与圆锥曲线的综合问题,解题时要认真审题,仔细解答,注意公式的灵活运用.
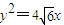 的焦点
的焦点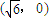 ,又椭圆C上有一点M(2,1),由此可求出椭圆方程.
,又椭圆C上有一点M(2,1),由此可求出椭圆方程.(2)设直线在y轴上的截距为m,则直线
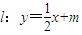 ,由直线l与椭圆C交于A、B两点,可导出m的取值范围是{m|-2<m<2且m≠0},设MA、MB的斜率分别为K1,K2,K1+K2=0,然后结合题设条件和根与系数的关系知MA,MB与x轴始终围成等腰三角形,从而得到m的取值范围.
,由直线l与椭圆C交于A、B两点,可导出m的取值范围是{m|-2<m<2且m≠0},设MA、MB的斜率分别为K1,K2,K1+K2=0,然后结合题设条件和根与系数的关系知MA,MB与x轴始终围成等腰三角形,从而得到m的取值范围.解答:解:(1)抛物线
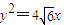 的焦点
的焦点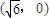 ,又椭圆C上有一点M(2,1)∴椭圆方程为,
,又椭圆C上有一点M(2,1)∴椭圆方程为,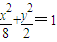
(2)
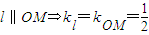 ,设直线在y轴上的截距为m,则直线
,设直线在y轴上的截距为m,则直线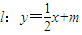
直线l与椭圆C交于A、B两点,
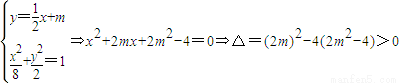
∴m的取值范围是{m|-2<m<2且m≠0},设MA、MB的斜率分别为K1,K2,∴K1+K2=0,
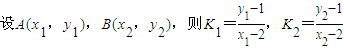 ∵
∵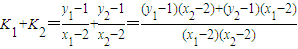
=
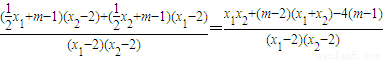
=
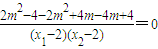
故MA,MB与x轴始终围成等腰三角形.∴m的取值范围是{m|-2<m<2且m≠0}
点评:本题考查直线与圆锥曲线的综合问题,解题时要认真审题,仔细解答,注意公式的灵活运用.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
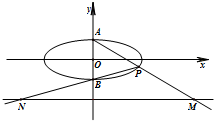 在平面直角坐标系xOy中,如图,已知椭圆C:
在平面直角坐标系xOy中,如图,已知椭圆C: 如图,已知椭圆
如图,已知椭圆 的上、下顶点分别为A、B,点P在椭圆C上且异于点A、B,直线AP、PB与直线l:y=-2分别交于点M、N.
的上、下顶点分别为A、B,点P在椭圆C上且异于点A、B,直线AP、PB与直线l:y=-2分别交于点M、N.
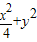 =1的上、下顶点分别为A、B,点P在椭圆C上且异于点A、B,直线AP、BP与直线l:y=-2分别交于点M、N;
=1的上、下顶点分别为A、B,点P在椭圆C上且异于点A、B,直线AP、BP与直线l:y=-2分别交于点M、N;
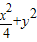 =1的上、下顶点分别为A、B,点P在椭圆C上且异于点A、B,直线AP、BP与直线l:y=-2分别交于点M、N;
=1的上、下顶点分别为A、B,点P在椭圆C上且异于点A、B,直线AP、BP与直线l:y=-2分别交于点M、N;