题目内容
过点 的直线
的直线 交直线
交直线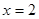 于
于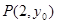 ,过点
,过点 的直线
的直线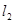 交
交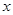 轴于
轴于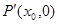 点,
点,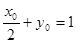 ,
,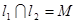 .
.
(1)求动点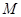 的轨迹
的轨迹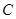 的方程;
的方程;
(2)设直线l与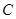 相交于不同的两点
相交于不同的两点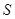 、
、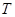 ,已知点
,已知点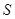 的坐标为(-2,0),点Q(0,
的坐标为(-2,0),点Q(0,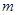 )在线段
)在线段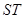 的垂直平分线上且
的垂直平分线上且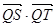 ≤4,求实数
≤4,求实数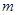 的取值范围.
的取值范围.
(1) 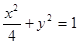
 ;(2)综上所述,
;(2)综上所述,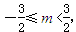 且
且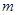 ≠0.
≠0.
解析试题分析:(1)由题意,直线 的方程是
的方程是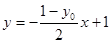 ,∵
,∵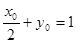 ,∴
,∴ 的方程是
的方程是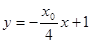
若直线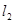 与
与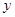 轴重合,则
轴重合,则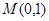 ,若直线
,若直线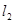 不与
不与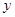 重合,可求得直线
重合,可求得直线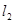 的方程是
的方程是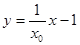 ,与
,与 的方程联立消去
的方程联立消去 得
得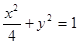 ,因
,因 不经过
不经过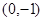 ,故动点动
,故动点动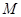 的轨迹
的轨迹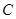 的方程是
的方程是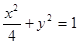
 6分
6分
(2)设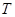 (x1,y1),直线l的方程为y=k(x+2)
(x1,y1),直线l的方程为y=k(x+2) 于是
于是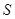 、
、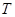 两点的坐标满足方程组
两点的坐标满足方程组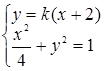 由方程消去y并整理得(1+4k2)x2+16k2x+16k2-4=0由-2x1=
由方程消去y并整理得(1+4k2)x2+16k2x+16k2-4=0由-2x1=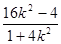 得x1=
得x1=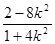 ,从而y1=
,从而y1=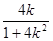 设线段
设线段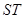 的中点为N,则N(
的中点为N,则N(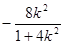 ,
,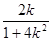 ) 8分
) 8分
以下分两种情况:①当k=0时,点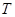 的坐标为(2,0),线段
的坐标为(2,0),线段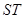 的垂直平分线为y轴,
的垂直平分线为y轴,
于是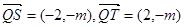 ,由
,由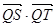 ≤4得:
≤4得: .
.
②当k≠0时,线段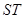 的垂直平分线方程为 y-
的垂直平分线方程为 y-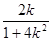 =-
=-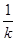 (x+
(x+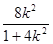 )令x=0,
)令x=0,
得m= ∵
∵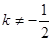 ,∴
,∴ ,
,
由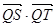 =-2x1-m(y1-m)=
=-2x1-m(y1-m)=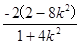 +
+ 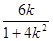 (
(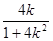 +
+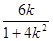 )=
)= ≤4
≤4
解得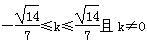 ∴m=
∴m= =
=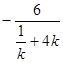 11分
11分
∴当
当 时,
时,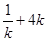 ≥4
≥4
∴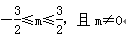
综上所述,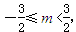 且
且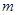 ≠0.…13分
≠0.…13分
考点:本题主要考查椭圆的方程,直线与椭圆的位置关系,平面向量的坐标运算,均值定理的应用。
点评:难题,曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。本题(1)求椭圆方程时,应用了参数法,并对可能的情况进行了讨论。(2)则在应用韦达定理的基础上,将m用k表示,并利用均值定理,逐步求得m的范围。

练习册系列答案
相关题目
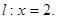 动圆M与定圆
动圆M与定圆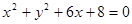 外切且与直线
外切且与直线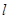 相切.
相切.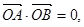 求证直线AB过一定点,并求出定点的坐标.
求证直线AB过一定点,并求出定点的坐标. =2x于M(x
=2x于M(x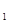 ,y
,y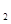 ,y
,y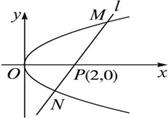
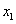 ,
,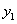 ),B(
),B(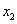 ,
,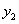 )是函数
)是函数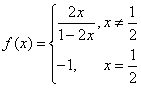 的图象上的任意两点(可以重合),点M在直线
的图象上的任意两点(可以重合),点M在直线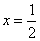 上,且
上,且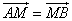 .
.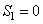 ,当
,当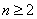 时,
时,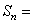
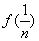 +
+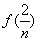 +
+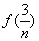 +
+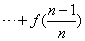 ,求
,求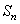 ;
;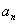 =
=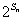 ,
,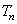 为数列{
为数列{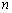 项和,若存在正整数
项和,若存在正整数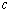 、
、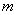 ,
,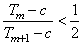 成立,求
成立,求 .
.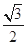 ,求椭圆的标准方程;
,求椭圆的标准方程; 的两个端点
的两个端点 、
、 分别分别在
分别分别在 轴、
轴、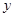 轴上滑动,
轴上滑动,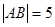 ,点
,点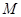 是
是 ,点
,点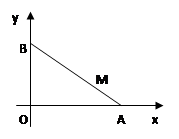
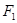 为点
为点 为右焦点,过
为右焦点,过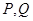 两点,求
两点,求 的最大值,并求此时直线
的最大值,并求此时直线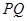 的方程.
的方程.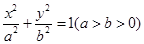 的两个焦点为F1、F2,点B1为其短轴的一个端点,满足
的两个焦点为F1、F2,点B1为其短轴的一个端点,满足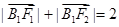 ,
,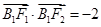 。
。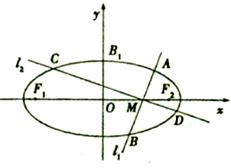
 做两条互相垂直的直线l1、l2设l1与椭圆交于点A、B,l2与椭圆交于点C、D,求的最小值。
做两条互相垂直的直线l1、l2设l1与椭圆交于点A、B,l2与椭圆交于点C、D,求的最小值。 经过抛物线
经过抛物线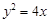 的焦点F,且与抛物线相交于A、B两点.
的焦点F,且与抛物线相交于A、B两点.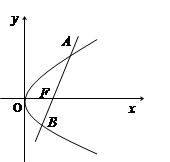
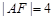 ,求点A的坐标;
,求点A的坐标;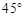 ,求线段AB的长.
,求线段AB的长.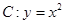 ,
,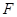 为焦点,
为焦点,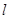 为准线,准线与
为准线,准线与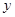 轴交点为
轴交点为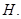
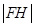 ;
;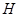 的直线与抛物线
的直线与抛物线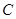 交于
交于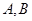 两点,直线
两点,直线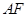 与抛物线交于点
与抛物线交于点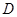 .
.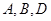 三点的横坐标分别为
三点的横坐标分别为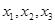 ,计算:
,计算: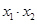 及
及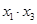 的值;
的值;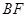 与抛物线交于点
与抛物线交于点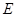 ,求证:
,求证: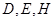 三点共线.
三点共线.