题目内容
已知函数y=f(x)满足: ;
;
(1)分别写出x∈[0,1)时y=f(x)的解析式f1(x)和x∈[1,2)时y=f(x)的解析式f2(x);并猜想x∈[n,n+1),n≥-1,n∈Z时y=f(x)的解析式fn+1(x)(用x和n表示)(不必证明)
(2)当![]() (n≥-1,n∈Z)时,y=fn+1(x)x∈[n,n+1),n≥-1,n∈Z的图象上有点列An+1(x,f(x))和点列Bn+1(n+1,f(n+1)),线段An+1Bn+2与线段Bn+1+An+2的交点Cn+1,求点Cn+1的坐标(an+1(x),bn+1(x));
(n≥-1,n∈Z)时,y=fn+1(x)x∈[n,n+1),n≥-1,n∈Z的图象上有点列An+1(x,f(x))和点列Bn+1(n+1,f(n+1)),线段An+1Bn+2与线段Bn+1+An+2的交点Cn+1,求点Cn+1的坐标(an+1(x),bn+1(x));
(3)在前面(1)(2)的基础上,请你提出一个点列Cn+1(an+1(x),bn+1(x))的问题,并进行研究,并写下你研究的过程
答案:
解析:
解析:
|
解:(1) (2)当 (3)(视问题的难易度给予不同的评分) 第一类(问题2分,解答2分) 例如:在(2)的条件下,点 解答: 第二类(问题3分,解答3分) 例如:在(2)的条件下,点 解答: 第三类(问题4分,解答4分) 例如:把(2)的条件 解答: |

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
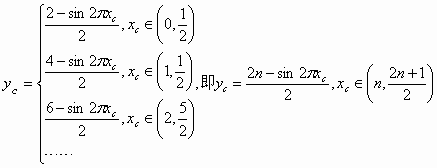 只需写出一个区间段上即可
只需写出一个区间段上即可 sinx在[0,π]上的大致图象是( )
sinx在[0,π]上的大致图象是( )


 )x-1.
)x-1.