题目内容
已知函数 在区间[-1,1),(1,3]内各有一个极值点.
在区间[-1,1),(1,3]内各有一个极值点.(Ⅰ)求a2-4b的最大值;
(Ⅱ)当a2-4b=8时,设函数y=f(x)在点A(1,f(1))处的切线为l,若在点A处穿过y=f(x)的图象(即动点在点A附近沿曲线y=f(x)运动,经过点A时,从l的一侧进入另一侧),求函数f(x)的表达式.
【答案】分析:(Ⅰ)极值点处的导数为零,导数在区间[-1,1),(1,3]各有一根
(Ⅱ)切线l在点A处穿过y=f(x)的图象,切线在该点的一侧在y=f(x)的图象上边,切线在该点的另一侧在y=f(x)的图象下边,构造函数该点不是新函数的极值点求值.
解答:解:(I)因为函数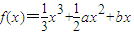 在区间[-1,1),(1,3]内分别有一个极值点,所以f'(x)=x2+ax+b=0在[-1,1),(1,3]内分别有一个实根,
在区间[-1,1),(1,3]内分别有一个极值点,所以f'(x)=x2+ax+b=0在[-1,1),(1,3]内分别有一个实根,
设两实根为x1,x2(x1<x2),则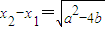 ,且0<x2-x1≤4.于是
,且0<x2-x1≤4.于是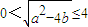 ,0<a2-4b≤16,且当x1=-1,x2=3,即a=-2,b=-3时等号成立.故a2-4b的最大值是16.
,0<a2-4b≤16,且当x1=-1,x2=3,即a=-2,b=-3时等号成立.故a2-4b的最大值是16.
(II)解法一:由f'(1)=1+a+b知f(x)在点(1,f(1))处的切线l的方程是y-f(1)=f'(1)(x-1),即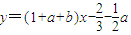 ,
,
因为切线l在点A(1,f(1))处穿过y=f(x)的图象,
所以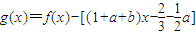 在x=1两边附近的函数值异号,则x=1不是g(x)的极值点.
在x=1两边附近的函数值异号,则x=1不是g(x)的极值点.
而g(x)=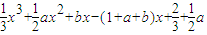 ,且g'(x)=x2+ax+b-(1+a+b)=x2+ax-a-1=(x-1)(x+1+a).
,且g'(x)=x2+ax+b-(1+a+b)=x2+ax-a-1=(x-1)(x+1+a).
若1≠-1-a,则x=1和x=-1-a都是g(x)的极值点.
所以1=-1-a,即a=-2.又由a2-4b=8,得b=-1.故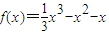 .
.
解法二:同解法一得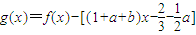 =
=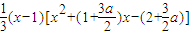 .
.
因为切线l在点A(1,f(1))处穿过y=f(x)的图象,所以g(x)在x=1两边附近的函数值异号.于是存在m1,m2(m1<1<m2).
当m1<x<1时,g(x)<0,当1<x<m2时,g(x)>0;
或当m1<x<1时,g(x)>0,当1<x<m2时,g(x)<0.
设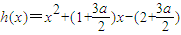 ,则
,则
当m1<x<1时,h(x)>0,当1<x<m2时,h(x)>0;
或当m1<x<1时,h(x)<0,当1<x<m2时,h(x)<0.
由h(1)=0知x=1是h(x)的一个极值点,则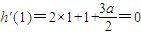 .
.
所以a=-2.又由a2-4b=8,得b=-1,故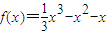 .
.
点评:本题考查利用导数求函数的极值,函数为极值的条件,构造函数能力.
(Ⅱ)切线l在点A处穿过y=f(x)的图象,切线在该点的一侧在y=f(x)的图象上边,切线在该点的另一侧在y=f(x)的图象下边,构造函数该点不是新函数的极值点求值.
解答:解:(I)因为函数
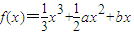 在区间[-1,1),(1,3]内分别有一个极值点,所以f'(x)=x2+ax+b=0在[-1,1),(1,3]内分别有一个实根,
在区间[-1,1),(1,3]内分别有一个极值点,所以f'(x)=x2+ax+b=0在[-1,1),(1,3]内分别有一个实根,设两实根为x1,x2(x1<x2),则
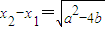 ,且0<x2-x1≤4.于是
,且0<x2-x1≤4.于是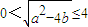 ,0<a2-4b≤16,且当x1=-1,x2=3,即a=-2,b=-3时等号成立.故a2-4b的最大值是16.
,0<a2-4b≤16,且当x1=-1,x2=3,即a=-2,b=-3时等号成立.故a2-4b的最大值是16.(II)解法一:由f'(1)=1+a+b知f(x)在点(1,f(1))处的切线l的方程是y-f(1)=f'(1)(x-1),即
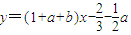 ,
,因为切线l在点A(1,f(1))处穿过y=f(x)的图象,
所以
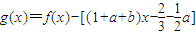 在x=1两边附近的函数值异号,则x=1不是g(x)的极值点.
在x=1两边附近的函数值异号,则x=1不是g(x)的极值点.而g(x)=
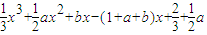 ,且g'(x)=x2+ax+b-(1+a+b)=x2+ax-a-1=(x-1)(x+1+a).
,且g'(x)=x2+ax+b-(1+a+b)=x2+ax-a-1=(x-1)(x+1+a).若1≠-1-a,则x=1和x=-1-a都是g(x)的极值点.
所以1=-1-a,即a=-2.又由a2-4b=8,得b=-1.故
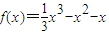 .
.解法二:同解法一得
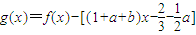 =
=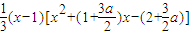 .
.因为切线l在点A(1,f(1))处穿过y=f(x)的图象,所以g(x)在x=1两边附近的函数值异号.于是存在m1,m2(m1<1<m2).
当m1<x<1时,g(x)<0,当1<x<m2时,g(x)>0;
或当m1<x<1时,g(x)>0,当1<x<m2时,g(x)<0.
设
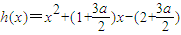 ,则
,则当m1<x<1时,h(x)>0,当1<x<m2时,h(x)>0;
或当m1<x<1时,h(x)<0,当1<x<m2时,h(x)<0.
由h(1)=0知x=1是h(x)的一个极值点,则
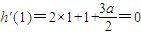 .
.所以a=-2.又由a2-4b=8,得b=-1,故
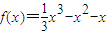 .
.点评:本题考查利用导数求函数的极值,函数为极值的条件,构造函数能力.

练习册系列答案
相关题目
 在区间[1,2]上不是单调函数,则错误!不能通过编辑域代码创建对象。的范围为
在区间[1,2]上不是单调函数,则错误!不能通过编辑域代码创建对象。的范围为 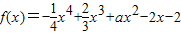 在区间[-1,1]上单调递减,在区间[1,2]上单调递增,
在区间[-1,1]上单调递减,在区间[1,2]上单调递增,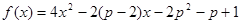 在区间[-1,1]上至少存在一个实数c使f(c)>0,则实数p的范围 .
在区间[-1,1]上至少存在一个实数c使f(c)>0,则实数p的范围 . 在区间[1,2]上不是单调函数,则错误!不能通过编辑域代码创建对象。的范围为
在区间[1,2]上不是单调函数,则错误!不能通过编辑域代码创建对象。的范围为