题目内容

8．求证：${C}_{n}^{0}$+2${C}_{n}^{1}$+3${C}_{n}^{2}$+…+（n+1）${C}_{n}^{n}$=2n+n•2n-1．

分析 利用组合数阶乘形式的公式得到kCnk=nCn-1k-1；将原式变成（Cn0+Cn1+Cn2+Cn3+…+Cnn）+n（Cn-10+Cn-11+Cn-12+Cn-13++Cn-1n-1），再利用二项式系数的和即可求解

解答 证明：∵kCnk=nCn-1k-1
∴${C}_{n}^{0}$+2${C}_{n}^{1}$+3${C}_{n}^{2}$+…+（n+1）${C}_{n}^{n}$=（Cn0+Cn1+Cn2+Cn3+…+Cnn）+n（Cn-10+Cn-11+Cn-12+Cn-13+…+Cn-1n-1）
=2n+n•2n-1
等式成立．

点评 本题考查组合数的公式性质：kCkn=nCk-1n-1；考查二项式系数和公式，属于基础题．

练习册系列答案
相关题目
18．某人从银行贷款100万元，以后每年还款13.5万元，10年还清，问银行贷款的年利率是多少？
19．正方形的四个顶点都在函数y=x3+mx的图象上，若满足条件的正方形只有一个，则实数m=-2$\sqrt{2}$．
16．化简（cos47°30′-sin47°30′）（sin23°cos8°-sin67°sin8°）=（　　）
A．$\frac{1}{4}$B．-$\frac{1}{4}$C．1D．-1
3．在△ABC中，若AB=1，BC=2，CA=$\sqrt{5}$，则$\overrightarrow{AB}$$•\overrightarrow{BC}$+$\overrightarrow{BC}$•$\overrightarrow{CA}$$+\overrightarrow{CA}$•$\overrightarrow{AB}$的值是-5．
13．已知变量x、y满足约束条件$\left\{\begin{array}{l}{|x|≤y}\\{x+2y-1≤0}\end{array}\right.$，则目标函数z=2x-y的最小值为（　　）
A．-3B．$\frac{1}{3}$C．-2D．0
4．已知曲线C1的极坐标方程p2=$\frac{12}{3co{s}^{2}θ+4si{n}^{2}θ}$，曲线C1经过坐标变换$\left\{{\begin{array}{l}{x=2x'}\\{y=\sqrt{3}y'}\end{array}}$得到曲线C2，直线l的参数方程为$\left\{{\begin{array}{l}{x=2+\frac{{\sqrt{2}}}{2}t}\\{y=\frac{{\sqrt{2}}}{2}t}\end{array}}$（t为参数，t∈R）
（Ⅰ）求直线l的普通方程和曲线C1的直角坐标方程；
（Ⅱ）若P为曲线C2上的点，求点P到直线l的距离的最大值．
1．将正方形ABCD沿对角线BD折成直二面角A-BD-C，有如下四个结论：
（1）AC⊥BD           （2）AB与平面BCD成60°的角
（3）△ACD是等边三角形 （4）AB与CD所成的角为60°
正确结论的编号是①③④．
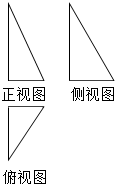2．一个几何体的三视图如图所示，其正视图、侧视图、俯视图均为直角三角形，且面积分别为$\frac{3}{2}$，3，1，则该几何体外接球的表面积为14π．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网