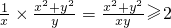题目内容
记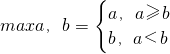 设
设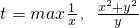 ,其中x,y∈R+,则t的最小值为________.
,其中x,y∈R+,则t的最小值为________.

分析:利用最大值的定义得到t≥
 >0,t≥
>0,t≥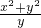 >0,利用不等式的性质得到t2≥
>0,利用不等式的性质得到t2≥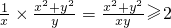 ,从而求出所求.
,从而求出所求.解答:∵
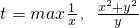 ,
,∴t≥
 >0,t≥
>0,t≥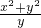 >0
>0即t2≥
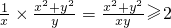
∴t≥

即t的最小值为

故答案为:

点评:本题主要考查了函数的最值及其几何意义,以及利用基本不等式求函数的最值,属于中档题.

练习册系列答案
相关题目
题目内容
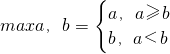 设
设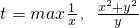 ,其中x,y∈R+,则t的最小值为________.
,其中x,y∈R+,则t的最小值为________.
 >0,t≥
>0,t≥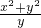 >0,利用不等式的性质得到t2≥
>0,利用不等式的性质得到t2≥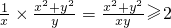 ,从而求出所求.
,从而求出所求.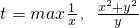 ,
, >0,t≥
>0,t≥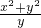 >0
>0